反比例函数复习课VIP免费

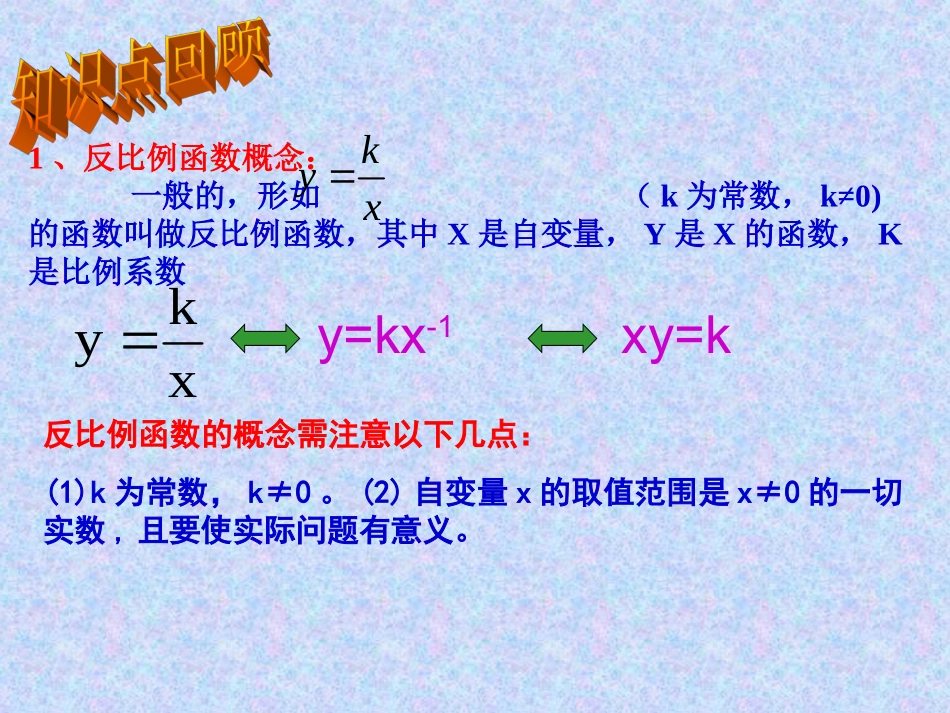
王朝辉王朝辉反比例函数复习课xy反比例函数的概念需注意以下几点：(1)k为常数，k≠0。(2)自变量x的取值范围是x≠0的一切实数,且要使实际问题有意义。xkyy=kx-1xy=k1、反比例函数概念：一般的，形如（k为常数，k≠0)的函数叫做反比例函数，其中X是自变量，Y是X的函数，K是比例系数kyx练一练11、在下列函数中，y是x的反比例函数的是（）（A）（B）+7（C）xy=5（D）2、已知函数是反比例函数,则m=___y=8X+5y=x3y=x2222(1)mymx-40-51-3yx2345-16-2-61y=Kxy0123123456y=Kx2．反比例函数的图象和性质．反比例函数(k为常数，k≠0）的图象是双曲线，具有如下的性质：①当k＞0时，双曲线的两支分别在第一、三象限，在每个象限内，y随x的增加而减小；②当k＜0时，双曲线的两支分别在第二、四象限，在每个象限内，y随x的增大而增大．kyx双曲线的两分支都无限的接近坐标轴，但是永远不能到达x轴、y轴。3.反比例函数的对称性反比例函数的图像——双曲线关于坐标原点中心对称，即双曲线一支上任意一点A(a,b)关于原点对称点A'(-a,-b)比在双曲线的另一支上。1.函数的图象在第_____象限，在每个象限内，y随x的增大而_____.2.双曲线经过点（-3，___）y=x5y=13x3.函数的图象在二、四象限，则m的取值范围是____.4.对于函数，当x<0时，y随x的_____而增大，这部分图象在第________象限.5.若点A（-2，y1)、B（-1，y2）c(1,y3)在反比例函数的图像上，则y1____y2____y3y=12xm-2xy=练习221myx6、如图，函数和y=－kx+1(k≠0)在同一坐标系内的图象大致是（）642-2-4-55Oyx642-2-4-55Oyx642-2-4-55Oyx642-2-4-55OyxBACD方法：先假设某个方法：先假设某个函数图象已经画好，函数图象已经画好，再确定另外的是否再确定另外的是否符合条件符合条件..xky以前做过这样的题目吗？例1已知反比例函数y=的图象与一次函数y=kx+m的图象相交于点(2,1)(1)分别求出这两个函数的解析式.(2)试判断点P(-1,2)关于x轴的对称点P’是否在反比例函数y=的图象上.xkxk•函数来自现实生活,函数是描述现实世界变化规律的重要数学模型.•函数的思想是一种重要的数学思想,它是刻画两个变量之间关系的重要手段.•从函数的图象中获取信息的能力是学好数学必需具有的基本素质.例2、为了预防某种传染疾病,某学校对教室采用药熏消毒法进行毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请根据题中所提供的信息,解答下列问题:(1)药物燃烧时,y关于x的函数关系式为:________,自变量x的取值范围是:_______,药物燃烧后y关于x的函数关系式为_______.(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过多少分钟后,学生才能回到教室;(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?6O8x(min)y(mg)y=3y=1.6巩固训练（2007年四川省成都市）如图，一次函数y=kx+b的图象与反比例函数的图象交A(-2,1),B(1,n)于两点．（1）试确定上述反比例函数和一次函数的表达式；(2)求的面积．myxAOB△课堂感悟课堂感悟谈谈你的收获与体会课后作业：作业纸