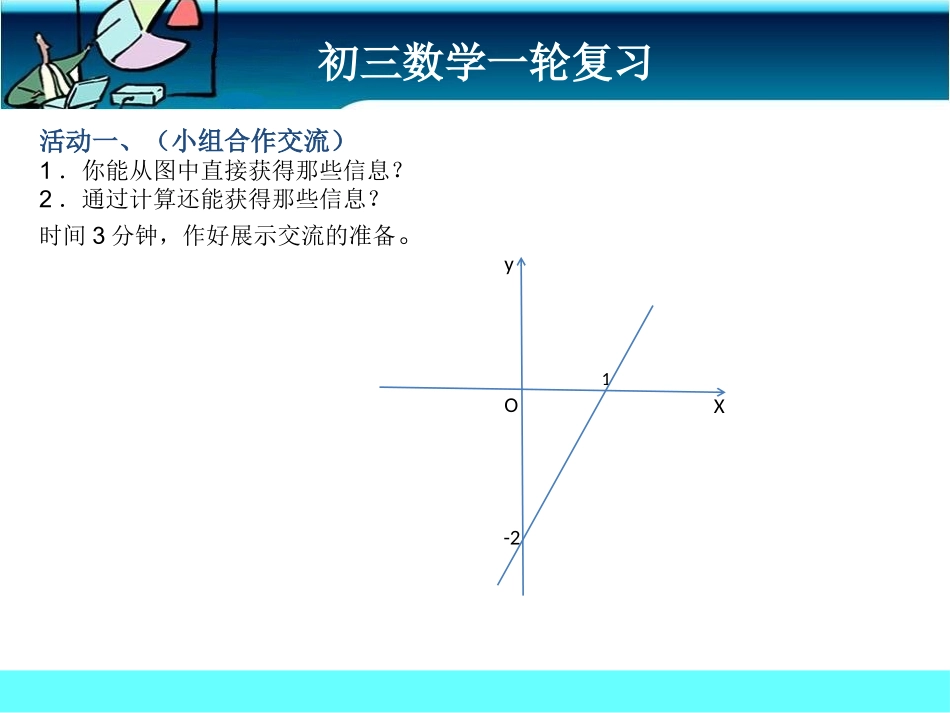
初三数学一轮复习一次函数活动一、(小组合作交流)1.你能从图中直接获得那些信息?2.通过计算还能获得那些信息?时间3分钟,作好展示交流的准备。初三数学一轮复习-21OyX活动二、学生展示直接可获得①A点坐标为(1,0),B点坐标为(0,-2).②AB是一条直线,对应的函数是一次函数.③函数y随x的增大而增大.④当x>1时,y>0;当x=1时,y=0;当x<1时,y<0.通过计算可获得⑤直线AB的解析式:y=2x-2.⑥直线AB与坐标轴围成的三角形面积=2.请你思考:直线AB向平移个单位过坐标原点.此时图像对应的函数是什么函数?它与一次函数的有怎样的关系?初三数学一轮复习活动三、考点梳理1.概念:形如函数y=kx+b(k、b都是常数,且k≠0)叫做一次函数,其中x是自变量.特别地,当b=0时,则把函数y=kx叫做正比例函数.2.正比例函数y=kx的图象:过(0,0),(1,k)两点的一条直线.3.正比例函数y=kx的性质:(1)当k>0时,y随x的增大而增大;(2)当k<0时,y随x的增大而减小.4.一次函数y=kx+b的图象:初三数学一轮复习初三数学一轮复习5.一次函数y=kx+b的性质:(1)当k>0时,y随x的增大而增大;(2)当k<0时,y随x的增大而减小求一次函数解析式的方法待定系数法是求一次函数解析式的常用方法,一般是先设待求的函数关系式(其中含有未知常数),再根据条件列出方程或方程组,通过解方程或方程组,求出未知系数,从而得到所求函数解析式的方法.两个区别(1)正比例函数和一次函数的区别正比例函数是一次函数的特殊情况,一次函数包括正比例函数.也就是说:如果一个函数是正比例函数,那么一定是一次函数,但是,一个函数是一次函数,不一定是正比例函数.(2)正比例和正比例函数的区别成正比例的两个量之间的函数关系不一定是正比例函数,但正比例函数的两个量一定成正比例.活动四、考点巩固测试1.对于一次函数y=-2x+4,下列结论错误的是()A.函数值随自变量的增大而减小B.函数的图象不经过第三象限C.函数的图象向下平移4个单位长度得y=-2x的图象D.函数的图象与x轴的交点坐标是(0,4)解析A. 一次函数y=-2x+4中k=-2<0,∴函数值随x的增大而减小,故本选项正确;B. 一次函数y=-2x+4中k=-2<0,b=4>0,∴此函数的图象经过一、二、四象限,不经过第三象限,故本选项正确;C.由“上加下减”的原则可知,函数的图象向下平移4个单位长度得y=-2x的图象,故本选项正确;D. 令y=0,则x=2,∴函数的图象与x轴的交点坐标是(2,0),故本选项错误.感悟提高根据一次函数的性质,若已知系数k的符号就可以直接说出函数y的值随x增大的增减情况(即增减性);反之,若知道一次函数的增减性,就能推断系数k的符号;一次函数的图象直线y=kx+b与y轴交点(0,b),根据交点的位置,就能推断b的符号.初三数学一轮复习变式测试1(1)(2013·衡阳)如图,一次函数y=kx+b的图象与x轴的交点坐标为(2,0),则下列说法:①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2.其中说法正确的有________.(把你认为说法正确的序号都填上)(2)已知一次函数y=3x+m-2的图象不经过第二象限,则m的取值范围是________.解析 直线不经过第二象限,∴m-2<0,m<2.初三数学一轮复习2.如图,直线l1、l2相交于点A(2,3),直线l1与x轴的交点坐标为(-1,0),直线l2与y轴的交点坐标为(0,-2),结合图象解答下列问题:(1)求直线l1、l2的解析式;解设直线l1的解析式为y1=k1x+b1有∴y1=x+1.同理:直线l2的解析式为y2=(5/2)x-2.(2)求直线l1、l2与y轴围成的三角形的面积.解直线l1:y1=x+1与y轴交于点(0,1);直线l2:y2=(5/2)x-2与y轴交于点(0,-2).∴三角形的面积=(1/2)×[1-(-2)]×2=3.感悟提高k、b是一次函数y=kx+b的未知系数,这种先设待求函数关系式,再根据条件列出方程或方程组,求出未知数,从而得出所求结果的方法,就是待定系数法初三数学一轮复习变式测试2如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.(1)求线段AB所在直线的函数解析式,并写出当0≤y≤2时,自变量x的取值范围;(2)将线段AB绕点B逆时针旋转90°,得到线段BC,请画出线段BC...