《勾股定理应用（已修改）》课件VIP免费

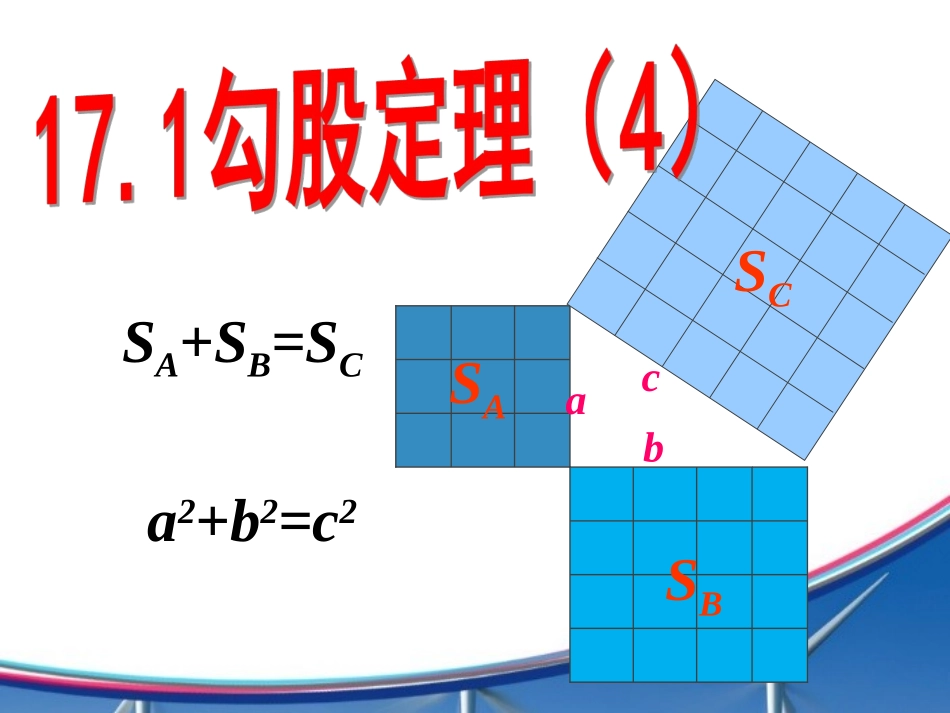
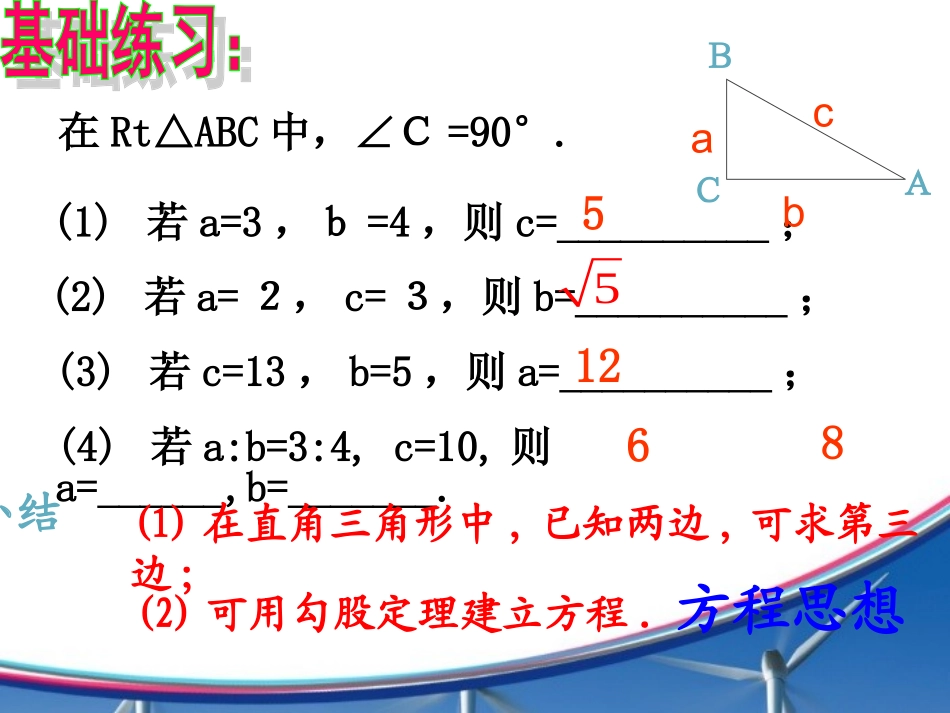
SA+SB=SCa2+b2=c2abcSASBSCcab在△ABC中，∠C=90°.(4)斜边大于直角边;(1)两锐角互余;(2)30°角所对的直角边等于斜边的一半;CAB(3)勾股定理：a2+b2=c2直角三角形两直角边a、b平方和，等于斜边c平方。(2)可用勾股定理建立方程.(2)若a=２，c=３，则b=__________；(3)若c=13，b=5，则a=__________；(4)若a:b=3:4,c=10,则a=______,b=_______.(1)若a=3，ｂ=4，则c=__________；在Rt△ABC中，∠Ｃ=90°.zxxkabcＡＣＢ小结(1)在直角三角形中,已知两边,可求第三边;512568方程思想思维拓展：有没有一种直角三角形，已知一边可以求另外两边长呢？ACBbac45°ACBbac30°a:b:c=1:1:2a:b:c=1::231、已知：Rt△ＡBC中，AB＝４，AC＝３,则BC的长为.5或743ACB43CAB分类讨论2.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BCzxx```k∟D∟DABCABC1017817108分类讨论小明想知道学校旗杆的高，他发现旗杆顶端的绳子垂到地面还多1米，当他把绳子的下端拉开5米后，发现下端刚好接触地面，求旗杆的高度。x+1x52225(1)xx222521xxx2251x12x1练习&&11☞☞方程思想1.小溪边长着两棵树，恰好隔岸相望，一棵树高30尺，另外一棵树高20尺；两棵树干间的距离是50尺，每棵树上都停着一只鸟，忽然两只鸟同时看到两树间水面上游出一条鱼，它们立刻以同样的速度飞去抓鱼，结果同时到达目标。问这条鱼出现在两树之间的何处？zx111xk3020x50-x22223020(50)xx20()x解得尺方程思想2.在△ABC中，AB=15，BC=14，AC=13，求(1)ABC△的面积；(2)求腰AC上的高zx===xkABC151413Dx14-x22221513(14)xx22221513(14)xx28214(214)x9x解得222215912ADABBD1212ABCSBCAD11412842E方程思想面积法1.在ABC中,∠C=90°,AC=6,CB=8,则ABC面积为_____,斜边为上的高为______.244.8AABBCCDD练习&&22☞☞面积法zx===xk2.已知:一个三角ABC,AB=AC=13,BC=10,(1)求它的面积；(2)求腰AC上的高.ABC13135512DE12ABCSBCAD110126021602ABCSACBE13120BE12013BE如果电梯的长、宽、高分别是1.5米、1.5米、2.2米，那么，能进入电梯内的竹竿的最大长度大约是多少米？练习3:1.5米1.5米2.2米1.5米1.5米2.2米1.5米1.5米xx2.2米ABCX2=1.52+1.52=4.5AB2=2.22+X2=9.34AB≈3米zx···xk如图，是一个三级台阶，它的每一级的长、宽和高分别等于5cm，3cm和1cm，A和B是这个台阶的两个相对的端点，A点上有一只蚂蚁，想到B点去吃可口的食物.请你想一想，这只蚂蚁从A点出发，沿着台阶面爬到B点，最短线路是多少？BAABC531512一、台阶中的最值问题 AB2=AC2+BC2=169,∴AB=13.学·科·网变式3：如果盒子换成如图长为3cm，宽为2cm，高为1cm的长方体，蚂蚁沿着表面需要爬行的最短路程又是多少呢？Z·x···xkAB321分析：有3种情况,六条路线。(1)经过前面和上底面;(或经过后面和下底面)(2)经过前面和右面;(或经过左面和后面)(3)经过左面和上底面.(或经过下底面和右面)AB23AB1C321BCA321BCA321例2、如图，长方体的长为15cm，宽为10cm，高为20cm，点B到点C的距离为5cm，一只蚂蚁如果要沿着长方体的表面从A点爬到B点，需要爬行的最短距离是多少？201015BCA分析：根据题意分析蚂蚁爬行的路线有两种情况(如图①②),由勾股定理可求得图1中AB最短.①BA2010155AB=√202+152=√625BAB=√102+252=√725②A2010155练习1:一只蚂蚁从实心长方体的顶点A1出发，沿长方体的表面爬到对角顶点C处（三条棱长如图所示），问怎样走路线最短？最短路线长为多少？ABA1B1DCD1C1214如果长方形的长、宽、高分别是a、b、c（a＞b＞c），你能求出蚂蚁从顶点A1到C的最短路径吗？A1B1145A1A41221(42)37224(21)537A1D142222(41)2929abc252937第一种路线最短ABA1B1DCD1C1bcaA1B1caA1AacA1D1ab从A1到C的最短路径是22()abc变式:如果长方形的长、宽、高分别是a、b、c（a＞b＞c），你能求出蚂蚁从顶点A1到C的最短路径吗？22222()2abcabcbc22222()2cababcab22222()2bacabcac0abcabacbc2222abcbc最小A1B1abc有一圆...