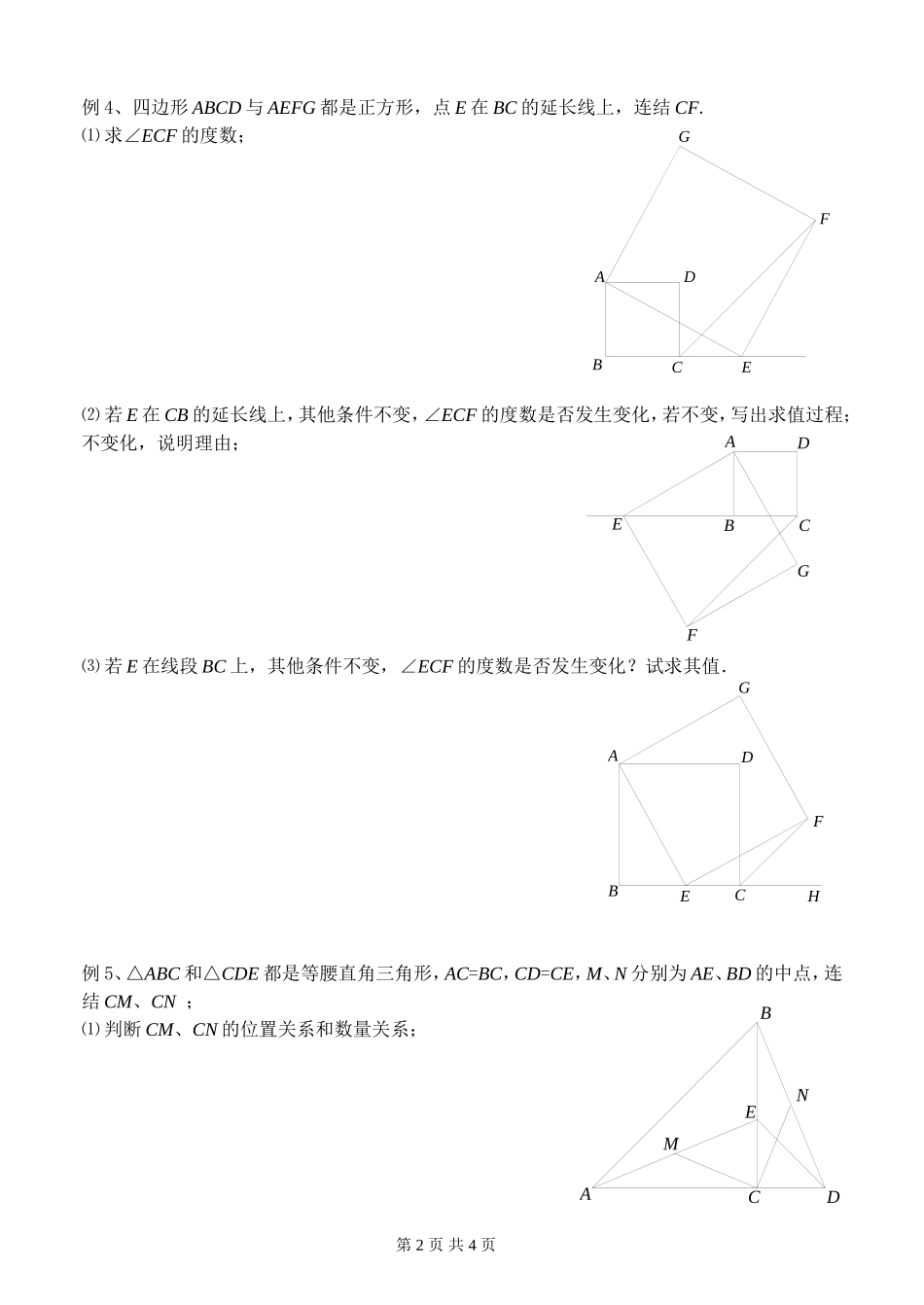
FGEDCBAFGEDCBAEDCBAEDCBA第四讲全等三角形图形研究例1、已知:AB=AC,AD=AE,AF⊥CD,AG⊥BE,求证:AF=AG.例2、已知:如图,BD、CE为△ABC的两条中线,延长BD到G,使BD=DG,延长CE到F,使CE=EF.⑴求证:AF=AG;⑵求证:F、A、G三点在同一条直线上.例3、如图:△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线.⑴作BD丄于D点,CE丄于E点,若B点和C点在直线的同侧,求证:BD=DE+CE.⑵若直线绕点A旋转到B点和C点在其两侧,其余条件不变,问BD、DE、CE的关系如何?请予以证明.第1页共4页FGEDCBAFGEDCBAFHGEDCBAMNEDCBA例4、四边形ABCD与AEFG都是正方形,点E在BC的延长线上,连结CF.⑴求∠ECF的度数;⑵若E在CB的延长线上,其他条件不变,∠ECF的度数是否发生变化,若不变,写出求值过程;不变化,说明理由;⑶若E在线段BC上,其他条件不变,∠ECF的度数是否发生变化?试求其值.例5、△ABC和△CDE都是等腰直角三角形,AC=BC,CD=CE,M、N分别为AE、BD的中点,连结CM、CN;⑴判断CM、CN的位置关系和数量关系;第2页共4页MNEDCBAEDCBAEDCBAPFQEDCBAP⑵若△CDE绕点C旋转任意角度,其他条件不变,则CM、CN的两种关系是否发生变化?试证明.例6、△ABC和△BDE都是等边三角形(三边、三角都相等),连结AE、CD相交于P.⑴求证:AE=CD;⑵求∠DPE的度数;⑶若△BDE绕点B旋转一定角度,其他条件不变,则⑴、⑵结论是否发生改变?试证明.例7、正方形ABCD中,45°的三角板BEF顶点放在B旋转,两边分别交AD、DC于P、Q.⑴判断PQ、AP、CQ三者之间的数量关系;⑵判断∠CQB和∠BQP的大小关系;第3页共4页EDCBAEDCBAFQEDCBAPxODCyPxOBAyPxOBAyP⑶△BEF的两边分别与正方形两边CD、DA的延长线相交,则⑴、⑵结论是否发生改变?试证明.例8、已知:如图,∠A=90°,BC=AC,DE为锐顶点A的任意直线,CD⊥DE于D,BE⊥DE于E.①若C,B在DE的两侧,求证:CD+BE=AD;②若C,B在DE的同侧,求证:│CD-BE│=AD;③若AE平分∠CAB,求证:AD=2BE;④若连结CE,求∠CEA.例9、⑴已知:P(4,4),将45°角的三角板,直角顶点放在P处,二边与坐标轴交于A、B二点.求证:PA=PB;⑵将三角板绕P点,顺时针旋转,二边与x轴交于B点与y轴交于A点间,OA-OB大小是否变化;⑶若将45°角放在P处,二边与x轴,y轴交于C、D.问①△OCD周长不变;②OC+OD不变.选择正确证明.第4页共4页