反比例函数应用（一）VIP免费

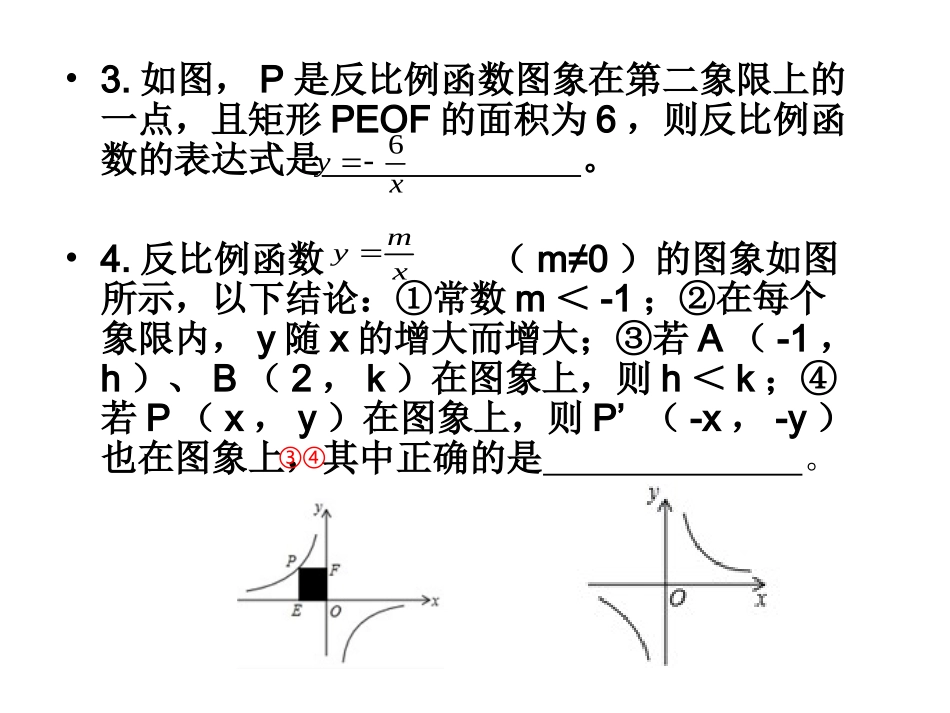
反比例函数的应用（一）新港城初级中学毛丽萍知识回顾•1.如果反比例函数的图象经过点P（-2，-1），那么这个反比例函数的表达式为。•2.若反比例函数的图象在其每一个象限内，y随x的增大而增大，则k的值可以是。（写出一个符合条件的值即可）2yxkyxK＜0-1•3.如图，P是反比例函数图象在第二象限上的一点，且矩形PEOF的面积为6，则反比例函数的表达式是。•4.反比例函数（m≠0）的图象如图所示，以下结论：①常数m＜-1；②在每个象限内，y随x的增大而增大；③若A（-1，h）、B（2，k）在图象上，则h＜k；④若P（x，y）在图象上，则P’（-x，-y）也在图象上，其中正确的是。6yx③④myx•5.如图，在平面直角坐标系中，反比例函数的图象与一次函数的图象交于A、B两点，若，则x的取值范围是。12yx2ykxb12yy＜1＜x＜3或x＜012yx┃考向互动探究┃►类型之一反比例函数与一次函数结合例1如图，一次函数y＝kx＋5(k为常数，且k≠0)的图象与反比例函数y＝－8x的图象交于A(－2，b)，B两点．(1)求一次函数的解析式；(2)若将直线AB向下平移m(m>0)个单位长度后与反比例函数的图象有且只有一个公共点，求m的值．y=kx+5y＝－8xAB对应训练如图，直线y＝kx＋2与反比例函数y＝22x(x>0)的图象交于点A，与坐标轴分别交于M，N两点，当AM＝MN时，k＝________．2►类型之二反比例函数与四边形结合例2如图,已知双曲线1-yx与两直线y=-14x、y=-kx（k＞0，且k≠14）分别相交于A、B、C、D四点,（1）当点C的坐标为（-1，1）时，A、B、D三点坐标分别是A（，），B（，），D（，）．（2）证明以点A、D、B、C为顶点的四边形是平行四边形．（3）当k为何值时，▱ADBC是矩形．∴D（1，-1），解得：x=2或-2故答案为：A(-2，),B(2,-),D(1,-1)1212解：（1）∵C（-1，1），C，D为双曲线与直线y=-kx的两个交点，且双曲线为中心对称图形，1yx1yx联立得：114yxyx消去y得：即114xx24x当x=2时，y=当x=-2时，y=1212A（-2，），B（2，）1212∴OA=OB，OC=OD，则以点A、D、B、C为顶点的四边形是平行四边形∵双曲线y=-为中心对称图形，且双曲线y=-与两直线y=-x，y=-kx（k＞0，且k≠）分别交于A、B、C、D四点，1x1x141423（2）如图1，∵四边形BQNC是菱形，∴BQ=BC=NQ，∠BQC=NQC∠，∵ABBQ⊥，C是AQ的中点∴BC=CQ=AQ，∴∠BQC=60°，∠BAQ=30°，在△ABQ和△ANQ中，∴△ABQANQ≌△，∴∠BAQ=NAQ=30°∠，∴∠BAO=30°，32∴OA=AB=3又∵P点在反比例函数的图象上，6yx∴P点坐标为（3,2）3∴AB=BQ=23课堂练习1．如图，在平面直角坐标系中，矩形OABC的顶点B坐标为（4,2），将矩形OABC绕点O逆时针旋转，使点B落在y轴上的点B′处，得到矩形OA′B′C′，OA′与BC相交于点D′，则经过点D的反比例函数解析式是．2．如图，在直角坐标系中，矩形OABC的顶点A、B在双曲线（x＞0）上，BC与x轴交于点D．若点A的坐标为(1，2)，则四边形OABD的面积为．kyx3．如图，正方形ABCD的顶点A、B分别在x轴、y轴的正半轴上，反比例函数kyx（k＞0）的图象经过另外两个顶点C、D，且点D（4，n）（0＜n＜4），则k的值为（）A.12B.8C.6D.4B4．如图，平行四边形OABC的顶点O在坐标原点，顶点A、C在反比例函数kyx（x>0）的图象上，点A的横坐标为4，点B的横坐标为6，且平行四边形OABC的面积为9，则k的值为____．65．如图，一次函数122yx的图象分别交x轴、y轴于A、B两点，P为AB的中点，PC⊥x轴于点C，延长PC交反比例函数kyx（x＜0）的图象于点Q，且tan∠AOQ=12．（1）求反比例函数的表达式；（2）连接OP、AQ，求证：四边形APOQ是菱形．