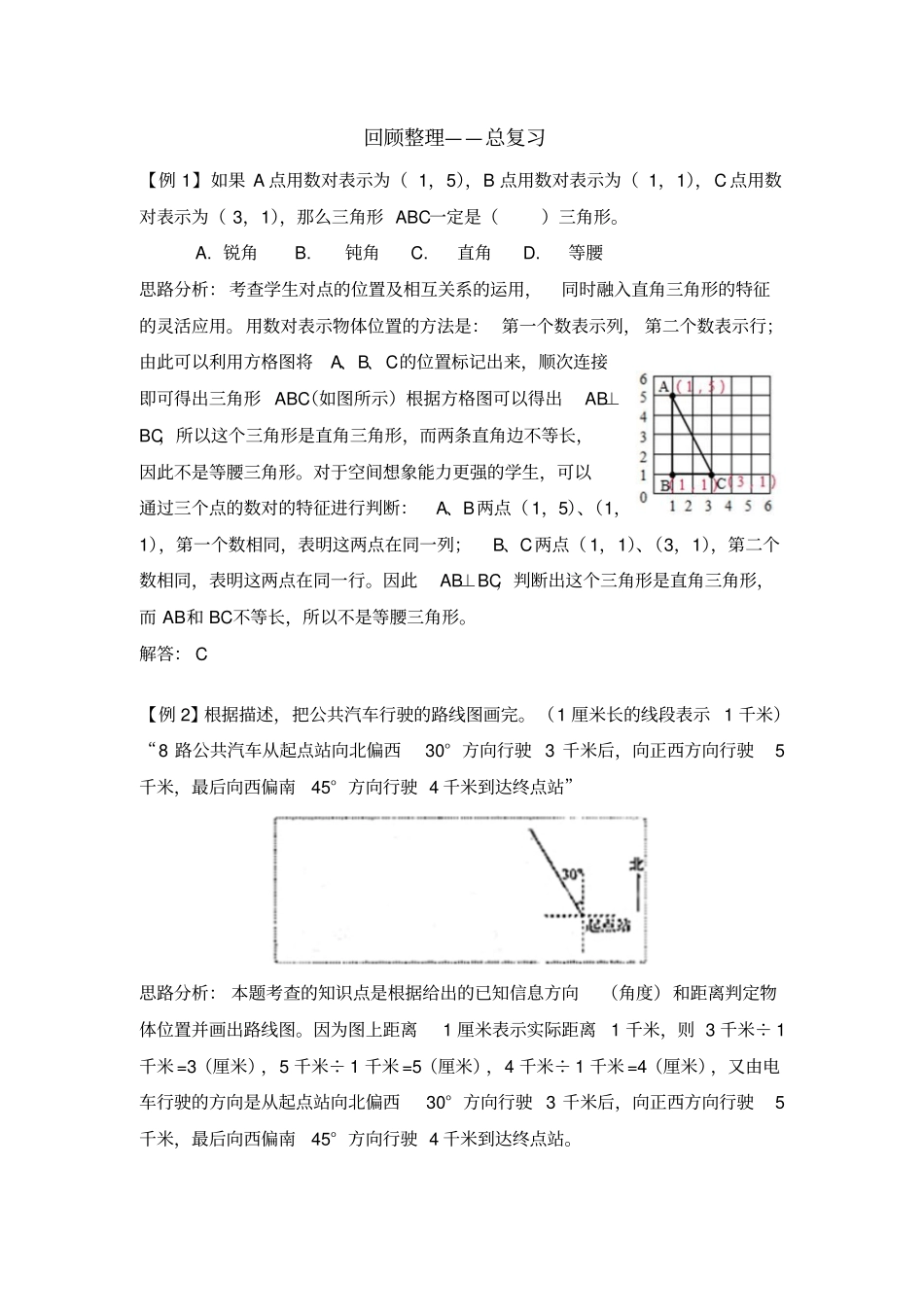
回顾整理——总复习【例1】如果A点用数对表示为(1,5),B点用数对表示为(1,1),C点用数对表示为(3,1),那么三角形ABC一定是()三角形。A.锐角B.钝角C.直角D.等腰思路分析:考查学生对点的位置及相互关系的运用,同时融入直角三角形的特征的灵活应用。用数对表示物体位置的方法是:第一个数表示列,第二个数表示行;由此可以利用方格图将A、B、C的位置标记出来,顺次连接即可得出三角形ABC(如图所示)根据方格图可以得出AB⊥BC,所以这个三角形是直角三角形,而两条直角边不等长,因此不是等腰三角形。对于空间想象能力更强的学生,可以通过三个点的数对的特征进行判断:A、B两点(1,5)、(1,1),第一个数相同,表明这两点在同一列;B、C两点(1,1)、(3,1),第二个数相同,表明这两点在同一行。因此AB⊥BC,判断出这个三角形是直角三角形,而AB和BC不等长,所以不是等腰三角形。解答:C【例2】根据描述,把公共汽车行驶的路线图画完。(1厘米长的线段表示1千米)“8路公共汽车从起点站向北偏西30°方向行驶3千米后,向正西方向行驶5千米,最后向西偏南45°方向行驶4千米到达终点站”思路分析:本题考查的知识点是根据给出的已知信息方向(角度)和距离判定物体位置并画出路线图。因为图上距离1厘米表示实际距离1千米,则3千米÷1千米=3(厘米),5千米÷1千米=5(厘米),4千米÷1千米=4(厘米),又由电车行驶的方向是从起点站向北偏西30°方向行驶3千米后,向正西方向行驶5千米,最后向西偏南45°方向行驶4千米到达终点站。解答:【例3】计算21+61+121+201+⋯+901。思路分析:本题考查的知识点是用拆数法计算异分母分数加法。解答时,先仔细观察算式中的每一个分数:这些分数的分子是1,分母是相邻的两个连续自然数的积。这些分数都可以拆成分子是1,分母是两个连续自然数的分数的差,如:21=211=1-21、61=321=21-31、⋯,这些分数相加后,前后两个分数的和是0。如:-21+21=0、-31+31=0、-41+41=0。解答:21+61+121+201+⋯+901=(1-21)+(21-31)+(31-41)+(41-51)+⋯+(91-101)=1-21+21-31+31-41+41-51+⋯+91-101=1-101=109【例4】一个长方体,底面是一个周长为12分米的正方形,侧面展开后是一个正方形,这个长方体的体积是()立方分米。A.144B.108C.36D.216思路分析:本题考查的知识点是用图示法计算长方体的体积。已知长方体底面是一个周长为12分米的正方形,侧面展开后是一个正方形,这说明长方体的高与底面周长相等,(如下图)也是12分米;这样先求出底面边长,再根据体积公式v=sh,代入数据计算出长方体的体积:12÷4=3(分米)、3×3×12=9×12=108(立方分米)。解答:B【例5】根据以下信息完成统计表。联系实际想一想,这样的天气情况说明了什么?思路分析:从已知信息中我们发现:6月份的天数是30天,其中阴天占51,根据求一个数的几分之几是多少用乘法计算,可以列式计算出阴天的天数是30×51=6(天),再结合晴天比阴天多占总天数的31,可以求出晴天的天数是6×(1+31)=8(天),这样可以得出雨天的天数是30-6-8=16(天),由此填写统计表并得出结论:雨天的天数大约占这个月的一半,其余天数约占一半。解答:结合统计表说明,这个月以晴天为主,阴天和雨天的天数和大约占这个月的一半。【例6】看图写算式并计算。(1)(2)思路分析:本题考查的知识点是利用“数形结合思想和图示法”来解答分数乘法要点提示读图表时,一般根据已有已知信息来步步分析推算其它信息。问题。解答时,先读懂线段图中给出的已知信息和所求的问题,然后利用数形结合思想分析已知信息和所求的问题之间的关系并找到问题的解答方法。(1)从图中读出:这条路400米是单位“1”,已经修了53,问题是求剩下的米数,求还剩下的米数就是求400米的(1-53)是多少,根据求一个数的几分之几是多少用乘法计算,列式计算为400×(1-53)=160(米)。(2)从图中读出,已知白菜有168吨,土豆比白菜多72,求土豆有多少吨,就是求比168多72的数是多少,根据求比一个数多几分之几的数是多少用乘法计算,列式计算为168×(1+72)=168×79=216(吨)。解答:(1)400×(1-53)=160...