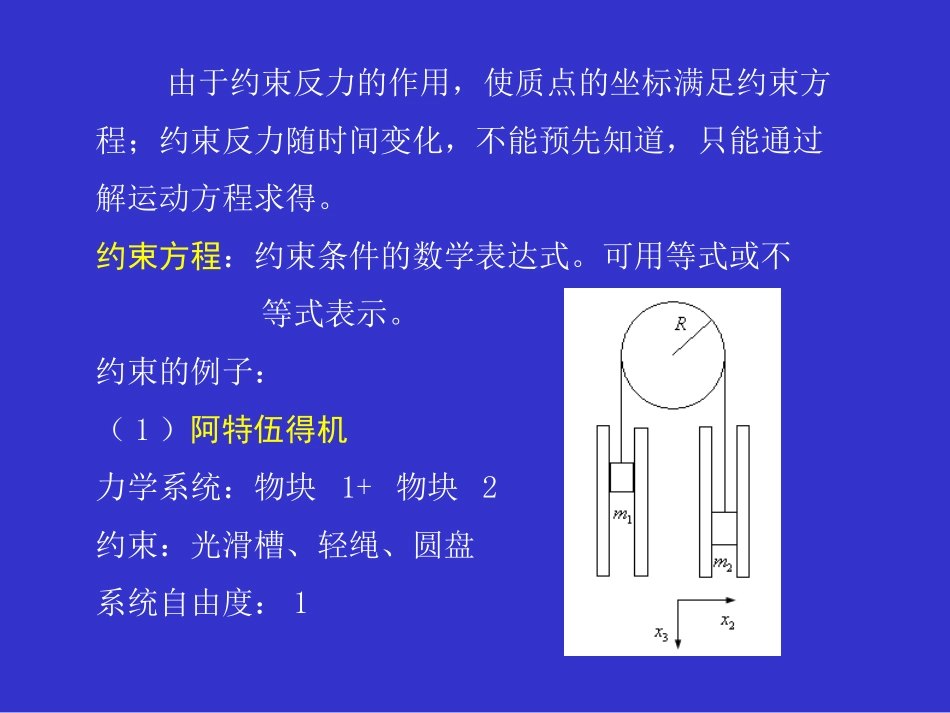
§1.1.2有约束情况下的拉格朗日方程讨论:受约束的多个质点在保守力场中的运动方程出发点:牛顿第二定律设:N个质点,质量和矢径分别是。牛顿运动方程:——3N个标量方程一般情况下,3N个方程并不独立。方程组不独立的原因:有约束的存在。约束的定义:力学系统在运动过程中受到的限制(包括对位置和速度的限制)。约束的作用:1.使力学系统的坐标之间发生关联而不全部独立;2.给力学系统施加约束反力。约束反力:约束总是通过一些外界物体(如轻杆、滑槽、软绳等)作用在所研究的系统中的质点上。在运动过程中,系统中的质点对这些外界物体有作用力,同时受到这些物体的反作用力,称为约束反力。由于约束反力的作用,使质点的坐标满足约束方程;约束反力随时间变化,不能预先知道,只能通过解运动方程求得。约束方程:约束条件的数学表达式。可用等式或不等式表示。约束的例子:(1)阿特伍得机力学系统:物块1+物块2约束:光滑槽、轻绳、圆盘系统自由度:1m1的坐标:;m2的坐标:——共6个坐标约束方程:(显示屏所在平面)——5个方程。(自由度=6-5=1)(2)单摆描述m的坐标:(不独立)约束方程:(两个独立)系统自由度:2——自由度数目少于坐标的数目N个质点的3N个笛卡尔坐标:若这些坐标满足3N-S个等式(约束方程):x:全部的独立方程的个数:3N-(3N-S)=S→力学体系只有S个独立坐标,即系统有S个自由度。约束的分类:1.约束方程中不含时间t——稳定约束2.约束方程中含时间t——不稳定约束3.由不等式表示的约束——可解约束4.由等式表示的约束——不可解约束约束的存在,使得力学系统的坐标不再独立→寻求独立坐标对于一个有S个自由度的力学系统,找到S个适合的变量,使3N个笛卡尔坐标是这S个变量的函数:以上函数关系满足约束方程,则这样的S个变量是决定系统中所有质点位置的独立变量,称为系统的广义坐标。广义坐标的引入解决了因约束方程相关联而不再全部独立的困难。例子:单摆中小球的直角坐标和摆角之间的关系。约束的存在,导致约束反力的存在,而约束反力不能预先知道,且很多时候并不关心约束反力→“消去”约束反力,只留下S个独立坐标所满足的方程。设:作用在第a个质点上的力为,写为::主动力;:约束反力。目标:“消去”约束反力。方法:引入虚位移、虚功。单摆的运动:质点只能在以悬点(固定)O为球心,以摆长L为半径的球面上运动。虚位移的定义:在任一时刻,约束所允许的位移称为虚位移,用表示。对单摆:虚位移在半径为L的球面的切面上(当虚位移很小时),约束反力沿球面的半径方向。显然,所以:定义虚功:实位移与虚位移的区别:实位移:同时满足运动规律和约束条件,在时间间隔dt内所发生的位移为实位移,它是唯一确定的。虚位移:设想在某一给定的时刻,在约束允许的条件下系统所发生的位移。虚位移并非发生在时间的流动过程中,它属于人为引入的位移,目的是为了处理未知的约束反力。虚位移不是运动学和动力学问题,而是一个几何问题。举例:(1)不稳定约束情况下,dr和的区别。不稳定约束:悬点作简谐振动的单摆虚位移在以t时刻悬点所在位置O(t)为心的球面上,实位移的起始点和终点分别在以O(t)和O(t+dt)为球心的两个球面上。显然:垂直,但不垂直。(2)阿特伍得机的虚位移:滑槽对的约束反力:(垂直滑槽表面)显然:软绳对的约束反力:显然:则:而所以结论:在理想的无耗散情况下,①约束反力所做的虚功为零;②各个质点所受到的约束反力所做的虚功之和为零。即定义:满足上式条件的约束称为理想约束。由得:()()()1()0NaaaaamFrr主——虚功原理文字表述:在理想约束情况下,作用在各个质点上的主动力和惯性力所做的虚功之和为零。对于平衡系统:则:对于保守系统,势能U为:作用在第a个质点上的主动力:比较前面单个质点的相应公式:结论:无约束时,实位移;有约束时,虚位移。现在由推导有约束情况下N个质点组成的系统的拉格朗日方程。对求微分:——对实位移对虚位移求变分:而虚位移是固定在某一时刻t不变时,约束所允许的位移,故,因此系统的动能:令L=T-U,则——拉格朗日方程§1.1.3最小作用量原理推导拉格朗日方...