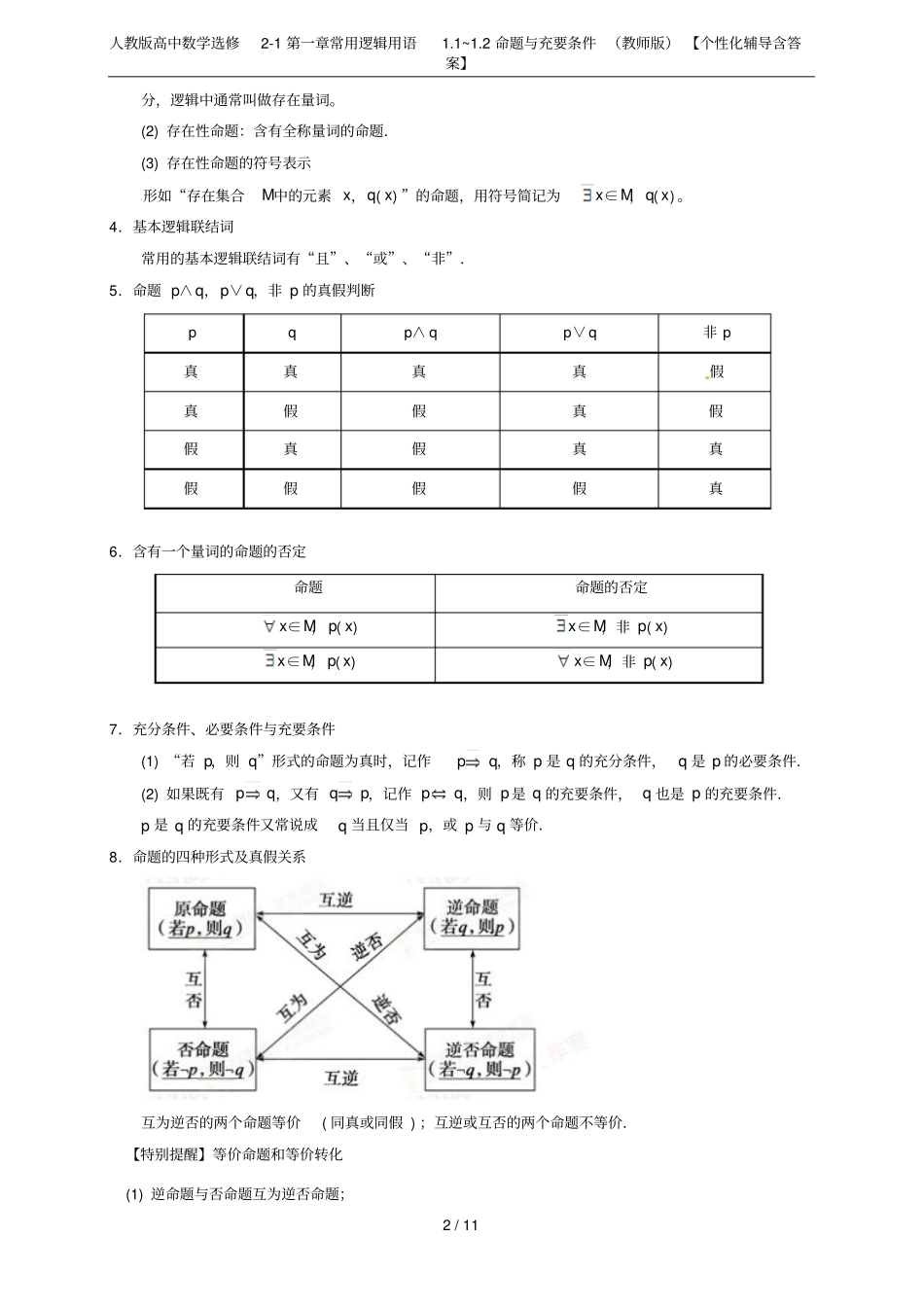
人教版高中数学选修2-1第一章常用逻辑用语1.1~1.2命题与充要条件(教师版)【个性化辅导含答案】1/11命题与充要条件____________________________________________________________________________________________________________________________________________________________________1理解四种命题及其相互关系,会判断四种命题的真假。2理解简单的逻辑联结词“或”“且”“非”的含义,能用“或”“且”“非”表述相关的数学内容。3会用“全称量词与存在量词”对命题进行否定。4理解充分条件、必要条件、充要条件等概念。5能够判断给定的两个命题的充要关系,充分条件与必要条件的判断。1.命题能判断真假的语句叫做命题.四种命题表述形式原命题:若p,则q逆命题:若q,则p否命题:若非p,则非q逆否命题:若非q,则非p2.全称量词与全称命题(1)全称量词:短语“所有”在陈述中表示所述事物的全体,在逻辑中通常叫做全称量词.(2)全称命题:含有全称量词的命题.(3)全称命题的符号表示形如“对M中所有x,p(x)”的命题,可用符号简记为“x∈M,p(x)”.3.存在量词与存在性命题(1)存在量词:短语“有一个”或“有些”或“至少有一个”在陈述中表示所述事物的个体或部人教版高中数学选修2-1第一章常用逻辑用语1.1~1.2命题与充要条件(教师版)【个性化辅导含答案】2/11分,逻辑中通常叫做存在量词。(2)存在性命题:含有全称量词的命题.(3)存在性命题的符号表示形如“存在集合M中的元素x,q(x)”的命题,用符号简记为x∈M,q(x)。4.基本逻辑联结词常用的基本逻辑联结词有“且”、“或”、“非”.5.命题p∧q,p∨q,非p的真假判断pqp∧qp∨q非p真真真真假真假假真假假真假真真假假假假真6.含有一个量词的命题的否定命题命题的否定x∈M,p(x)x∈M,非p(x)x∈M,p(x)x∈M,非p(x)7.充分条件、必要条件与充要条件(1)“若p,则q”形式的命题为真时,记作pq,称p是q的充分条件,q是p的必要条件.(2)如果既有pq,又有qp,记作pq,则p是q的充要条件,q也是p的充要条件.p是q的充要条件又常说成q当且仅当p,或p与q等价.8.命题的四种形式及真假关系互为逆否的两个命题等价(同真或同假);互逆或互否的两个命题不等价.【特别提醒】等价命题和等价转化(1)逆命题与否命题互为逆否命题;人教版高中数学选修2-1第一章常用逻辑用语1.1~1.2命题与充要条件(教师版)【个性化辅导含答案】3/11(2)互为逆否命题的两个命题同真假;(3)当判断原命题的真假比较困难时,可以转化为判断它的逆否命题的真假.类型一命题的四种形式及其关系例1:已知命题“若函数f(x)=ex-mx在(0,+∞)上是增函数,则m≤1”,则下列结论正确的是()A.否命题“若函数f(x)=ex-mx在(0,+∞)上是减函数,则m>1”是真命题B.逆命题“若m≤1,则函数f(x)=ex-mx在(0,+∞)上是增函数”是假命题C.逆否命题“若m>1,则函数f(x)=ex-mx在(0,+∞)上是减函数”是真命题D.逆否命题“若m>1,则函数f(x)=ex-mx在(0,+∞)上不是增函数”是真命题【解析】命题“若函数f(x)=ex-mx在(0,+∞)上是增函数,则m≤1”是真命题,所以其逆否命题“若m>1,则函数f(x)=ex-mx在(0,+∞)上不是增函数”是真命题.【答案】D练习1:给出命题“已知a、b、c、d是实数,若a=b,c=d,则a+c=b+d”,对其原命题、逆命题、否命题、逆否命题而言,真命题有()A.0个B.2个C.3个D.4个【解析】在四种命题中原命题和逆否命题同真假,故只需判断原命题和逆命题的真假即可.原命题为真.所以逆否命题为真.逆命题为“已知a、b、c、d是实数,若a+c=b+d,则a=b,c=d”,显然错误.所以否命题也错误.故真命题个数为2.【答案】B练习2:命题“若x,y都是偶数,则x+y也是偶数”的逆否命题是()A.若x+y是偶数,则x与y不都是偶数B.若x+y是偶数,则x与y都不是偶数C.若x+y不是偶数,则x与y不都是偶数D.若x+y不是偶数,则x与y都不是偶数【解析】若命题为“若p则q”,命题的逆否命题为“若非q,则非p”,所以原命题的逆否命题是“若x+y不是偶数,则x与y不都是偶数”。【答案】C类型二含有逻辑联结词命题真假的判断人教版高中数学选修2-1第一章...