同底数幂的乘法定稿VIP免费

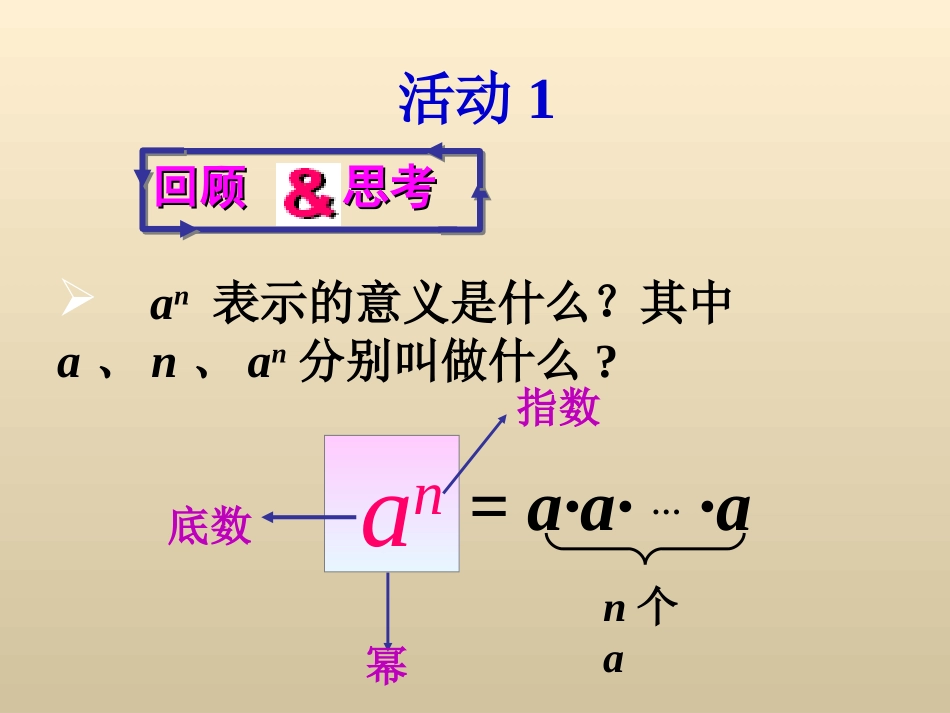
同底数幂的乘法教学目标1.理解同底数的乘法法则。2.运用同底数幂的乘法法则解决问题。3.通过“同底数幂的乘法法则”的推导和应用，使学生理解特殊到一般，一般到特殊的认知规律。回顾思考回顾思考=a·a·…·an个aan表示的意义是什么？其中a、n、an分别叫做什么?an底数幂指数活动1思考1.式子1015×103中的两个因数有何特点？2.为什么叫做同底数幂相乘？3.同底数幂相乘的法则是什么？am·an=am+n(当m、n都是正整数)am·an=m个an个a（aa…a）=aa…a=am+n(m+n)个a即am·an=am+n(当m、n都是正整数)（aa…a）（乘方的意义）（乘法结合律）（乘方的意义）am·an=am+n(当m、n都是正整数)同底数幂相乘，想一想：当三个或三个以上同底数幂相乘时，是否也具有这一性质呢？怎样用公式表示？底数，指数。不变相加同底数幂的乘法法则：请你尝试用文字概括这个结论。我们可以直接利用它进行计算.如43×45=43+5=48如am·an·ap=am+n+p（m、n、p都是正整数）运算形式运算方法（同底、乘法）（底不变、指加法）幂的底数必须相同，相乘时指数才能相加.智取百宝箱1.计算：（抢答）(1011)(a10)（x10）（b6）（2）a7·a3（3）x5·x5（4）b5·b（1）105×106Good!2.计算：（1）x10·x（2）10×102×104（3)x5·x·x3（4）y4·y3·y2·y解：（1）x10·x=x10+1=x11（2）10×102×104=101+2+4=107（3）x5·x·x3=x5+1+3=x9（4）y4·y3·y2·y=y4+3+2+1=y103.计算：(1)107×104(2)x2·x5(3)a·a6(4)xm·x2m+1(5)(-2)6·(-2)8(6)-26·(-2)8解：（1）107×104=107+4=1011（2）x2·x5=x2+5=x7（3）a·a6=a1+6=a7（5）(-2)6·(-2)8=(-2)6+8=(-2)14=214（4）xm·x2m+1=xm+m+1=x2m+1（6）-26·(-2)8=-26.28=-26+8=-2144.我是法官我来判（1）b5·b5=2b5（）（2）b5+b5=b10（）（3）（4）（5）c·c3=c3()（6）m+m3=m4()m+m3=m+m3b5·b5=b10b5+b5=2b5c·c3=c4××××了不起！11387)7(7733xxxx计算:（1）34)()(aaa解:原式=（-a)1+4+3=（-a)8(2)(x+y)3·(x+y)4am·an=am+n解:(x+y)3·(x+y)4=(x+y)3+4=(x+y)7公式中的a可代表一个数、字母、式子等.2、已知：am=2，an=3.求am+n=？.解：am+n=am·an（逆运算）=2×3=61、如果an-2an+1=a11,则n=.6同底数幂相乘，底数指数am·an=am+n(m、n正整数)整理反思我学到了什么？知识方法“特殊→一般→特殊”例子公式应用不变，相加.