解直角三角形的应用1VIP免费

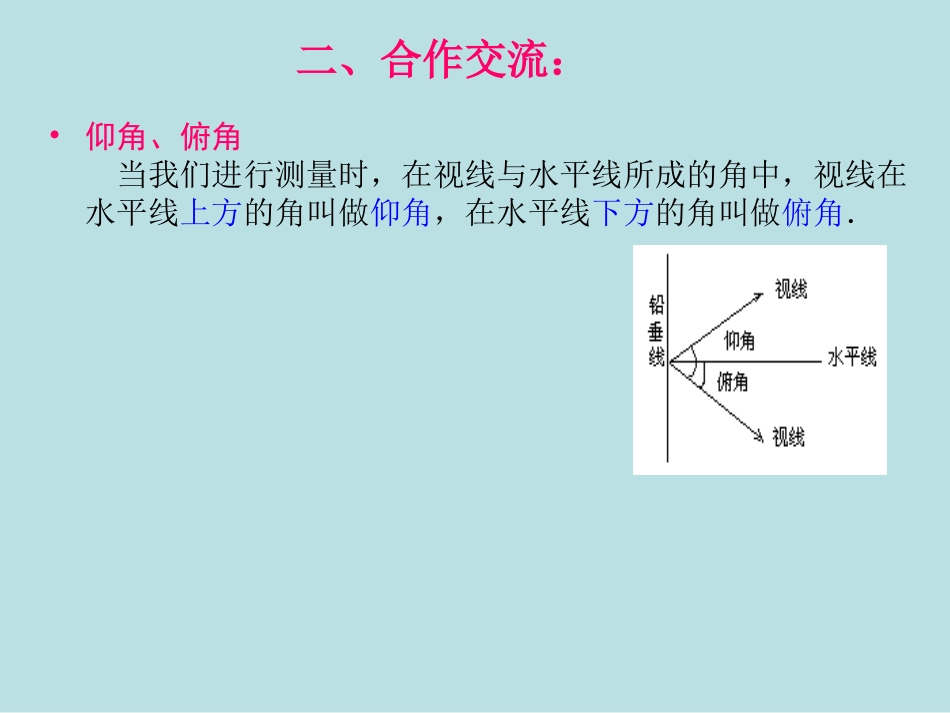
课题：28．2解直角三角形（2）【学习目标】⑴:使学生了解仰角、俯角的概念，使学生根据直角三角形的知识解决实际问题．⑵:逐步培养学生分析问题、解决问题的能力．⑶:渗透数学来源于实践又反过来作用于实践的观点，培养学生用数学的意识【学习重点】将某些实际问题中的数量关系，归结为直角三角形元素之间的关系，从而利用所学知识把实际问题解决．【学习难点】实际问题转化成数学模型【导学过程】•一、自学提纲：斜边的邻边AAcos斜边的对边AAsin的邻边的对边AA1．解直角三角形指什么？2．解直角三角形主要依据什么？(1)勾股定理：(2)锐角之间的关系：(3)边角之间的关系：tanA=二、合作交流：•仰角、俯角当我们进行测量时，在视线与水平线所成的角中，视线在水平线上方的角叫做仰角，在水平线下方的角叫做俯角．三、教师点拨：•例32003年10月15日“神舟”5号载人航天飞船发射成功.当飞船完成变轨后，就在离地球表面350km的圆形轨道上运行.如图,当飞船运行到地球表面上P点的正上方时，从飞船上最远能直接看到的地球上的点在什么位置?这样的最远点与P点的距离是多少?(地球半径约为6400km，结果精确到0.1km)•例4热气球的探测器显示，从热气球看一栋高楼顶部的仰角为30o，看这栋离楼底部的俯角为60o，热气球与高楼的水平距离为120m.这栋高楼有多高(结果精确到0.1m)?三、教师点拨：解：如图，a=30°,β=60°，AD＝120．ADCDADBDatan,tan30tan120tanaADBD3403312060tan120tanADCD312031203120340CDBDBC1.2773160答：这栋楼高约为277.1mABCDαβ四、学生展示：•课本93页练习第1、2题练习：练习：如图楼如图楼ABAB和楼和楼CDCD的水平距离为的水平距离为8800米，从楼顶米，从楼顶AA处测得楼顶处测得楼顶CC处的俯角为处的俯角为45°45°，测得楼底，测得楼底DD处的俯角为处的俯角为60°60°，试求，试求两楼高各为多少？两楼高各为多少？AABBCCDD45°AAEEDD（CC60°60°（8080米米EE练习：练习：如图楼如图楼ABAB和楼和楼CDCD的水平距离为的水平距离为8080米，从楼顶米，从楼顶AA处测得楼顶处测得楼顶CC处的俯角为处的俯角为45°45°，测得楼底，测得楼底DD处的俯角处的俯角为为60°60°，试求两楼高各为多少？，试求两楼高各为多少？45°AAEEDD（CC60°60°（8080米米五、课堂小结：•六、作业设置：•课本第96页习题28．2复习巩固第3、4题•七、自我反思：•本节课我的•收获:。