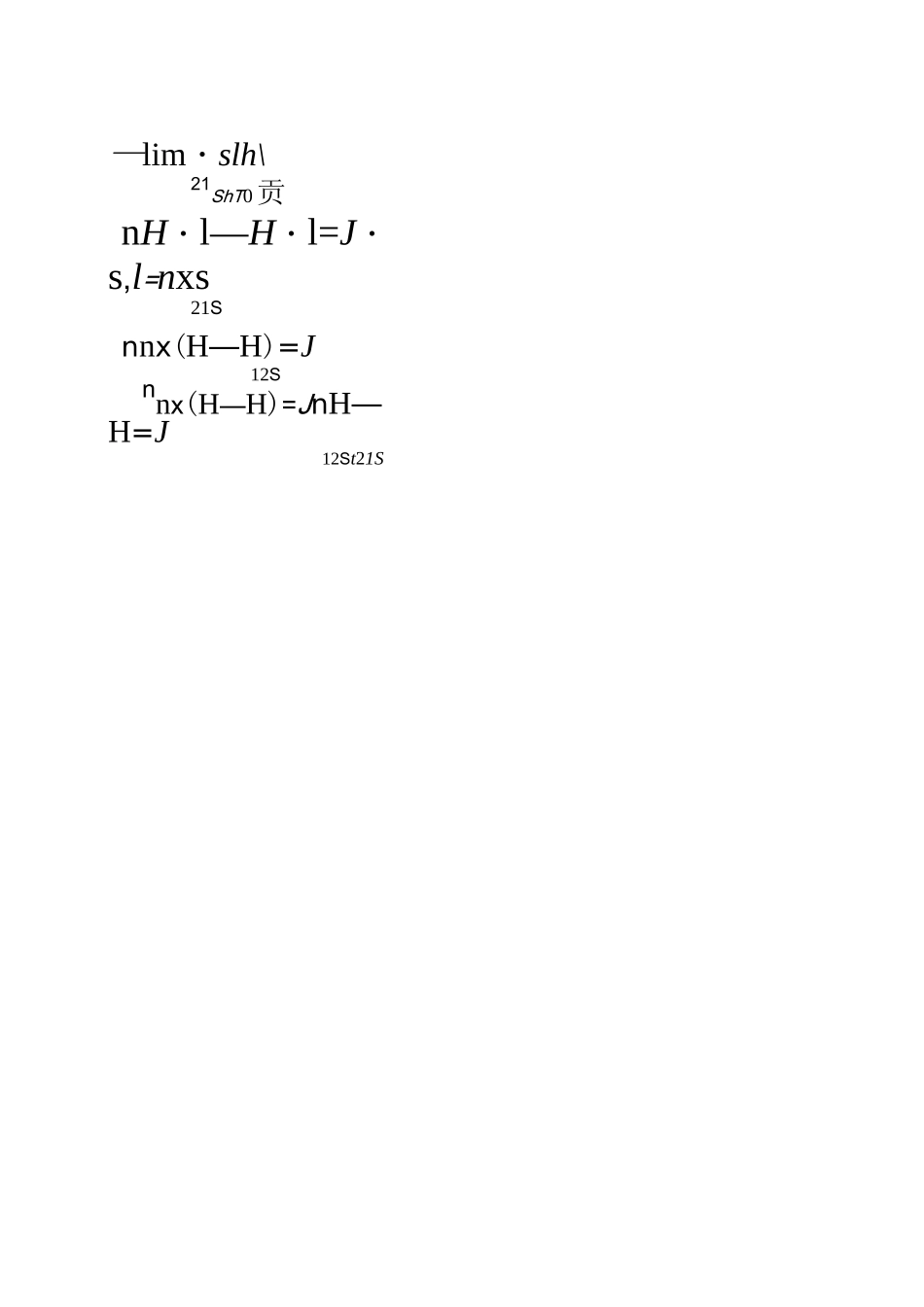3.H1)麦克斯韦方程组可以应用于任何连续的介质内部。2)在两种介质界面上,介质性质有突变,电磁场也会突变。3)分界面两边按照某种规律突变,称这种突变关系为电磁场的边值关系或边界条件。4)推导边界条件的依据是麦克斯韦方程组的积分形式。一、边界条件的一般形式1、B的边界条件:1B-dS=0・dS+B・dS=01122nB・n一B・n二012nB=B2n1nnn・(B1-B2)=0结论:电位移矢量在不同媒质分界面两侧的法向分量不连续,其差值等于分界面上自由电荷面密度。\HdDAhT0:6H.d广=J(J+贡).dS予•「•csD2/InH・l—H・l=J・sl(:)DdS=qSoD—D=o1n2n2、D的边界条件n(D—D)-n=◎12—lim・slh\21ShT0贡nH・l—H・l=J・s,l=nxs21Snnx(H—H)=J12Snnx(H—H)=JnH—H=J12St21SE0iAhT0"snnx(E—E)=00!E2:结nE=E1t21毎只分界面两侧的切向分量连p二0nx(E—E)=0\12nx(H—H)二0vi2n・(B—B)二0\12丿n・(D—D)二0J=0nE=E1t21nH二HnB1二B211n2nnD=D1n2n为介质分界面上的自由电流面密度。结论:磁场强度D在不同媒质分界面两侧的切向分量不连续,其差值等于分界面上的电流面密度J4.E的边界条件、E-dl=-J6B-dSiS~6f二、理想介质是指电导率为零的媒质,Y=02)在理想介质内部和表面上,不存在自由电荷和自由电流。结论:在理想介质分界面上,E、H矢量切向连续;在理想介质分界面上,B、D矢量法向连续三、理想导体表面上的边界条件1)理想介质是指电导率为无穷大的导体,2)电场强度和磁感应强度均为零。3)表面上,一般存在自由电荷和自由电流。设区域2为理想导体,区域1为介质,有DE,B,H均为零,得nxE=03E=20—itnxH1=J3H二J1StSn-B=03B=0nn-D1=◎3D=bSnS注意:理想介质和理想导体只是理论上存在。在实际应用中,某些媒质的电导率极小或极大,则可视作理想介质或理想导体进行处理。电磁场的边界条件可总结归纳如下:1)在两种媒质分界面上,如果存在面电流,使H切向分量不连续,其不连续量由式nx(H1-H2)=J确定若分界面上不存在面电流,则H的切向分量是连续的。2)在两种媒质的分界面上,E的切向分量是连续的。3)在两种媒质的分界面上,B的法向分量是连续的。4)在两种媒质的分界面上,如果存在面电荷,使D的法向分量不连续,其不连续量由n•(D-D)=o确定。若分界面上不存在面电荷,则D的法向分量是连续的。12积分形式::彳微分形式:电磁场的基本方程和边界条件基本方程积分形式:微分形式:积分形式:微分形式:1B-dS=0V-B=0^D-dS―qSV-D=p边界条件n-(B一B)=0v12n-(B1-B2)=0n-B]=0n・(D一D)=o\12n-(D1-D2)=0n-D1=0积分形式