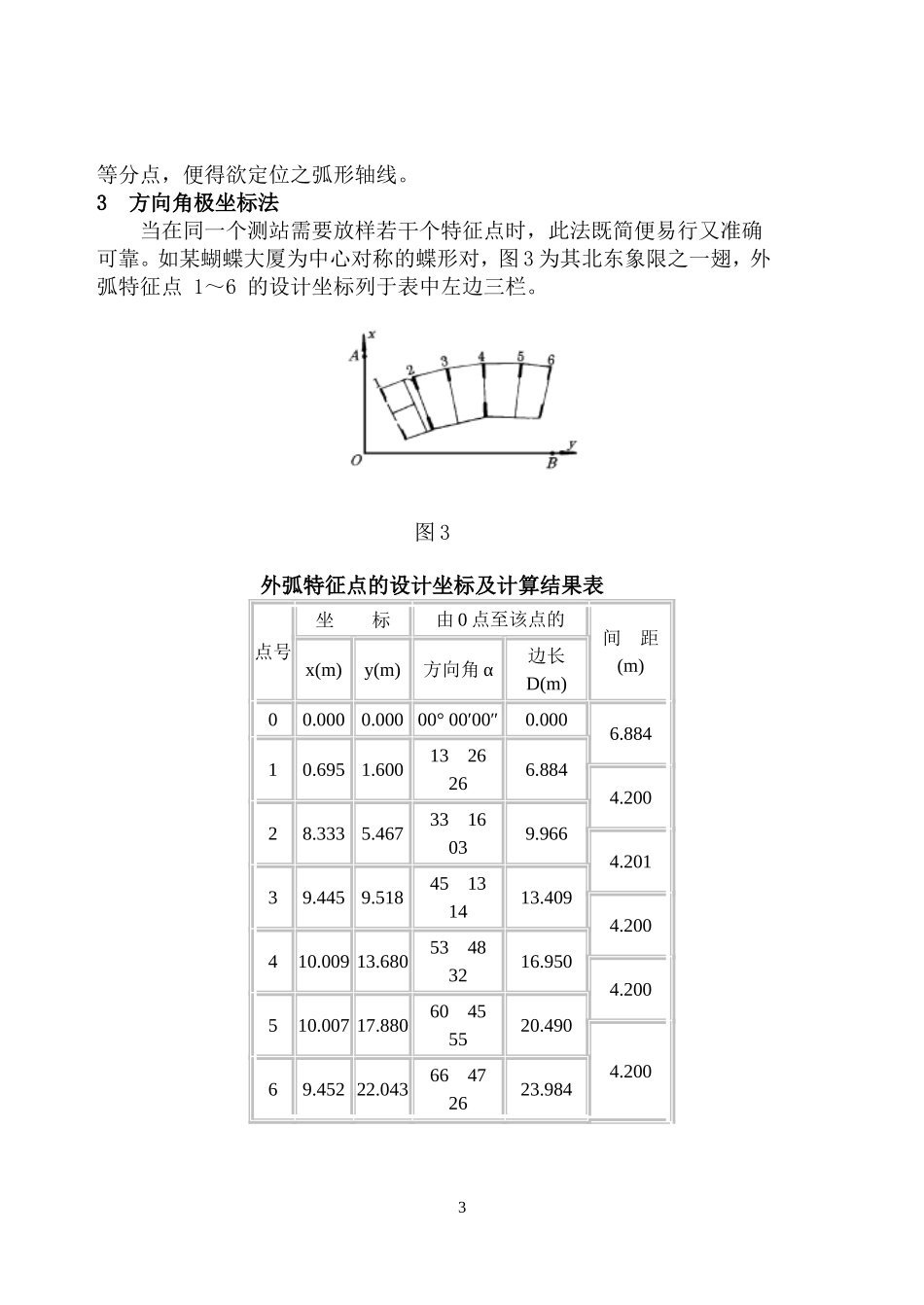
弧形建筑的定位方法[摘要]随着弧形公共建筑的日趋增多,讨论了在不同施工条件下弧形建筑的定位方法。[关键词]定位放样建筑设计规则设计近年来建筑平面设计呈弧形的公共建筑日趋增加。本文讨论弧形建筑的定位方法。1画弧拨角法当弧的半径较小时,此法简便易行。如某建筑平面呈半圆形,其定位条件如图1所示,D=35.000m,R=12.600m,进深L=5.600m。首先,根据道路中心线标定圆心O,然后以O为圆心,按内、外弧设计半径画弧,并且在O点安置经纬仪,按设计水平角拨角,放样各开间的辐射形轴线,依次标定各特征点。2拱高等分法当弧的半径较大,画弧不便时,可采用此法。如图2a,某建筑弧线的弦长为2do,拱高为lo。图11图2因已知放样数据弦长AB为2do,弧的拱高lo,故在AB的中点Oo放样垂距lo,标定弧的中点C。因(1)故可丈量BC,其值与设计值之相对精度应符合要求,以资检核。设弧的半径为R,则(2)令弦长BC=2d1(图2b),则BC弦的拱高(3)于是可在BC、AC的中点O1放样垂距l1,标定弧的四等分点M、N。逐次等分加密,直径加密点的间距满足施工要求,以平滑曲线连接各2等分点,便得欲定位之弧形轴线。3方向角极坐标法当在同一个测站需要放样若干个特征点时,此法既简便易行又准确可靠。如某蝴蝶大厦为中心对称的蝶形对,图3为其北东象限之一翅,外弧特征点1~6的设计坐标列于表中左边三栏。图3外弧特征点的设计坐标及计算结果表点号坐标由0点至该点的间距(m)x(m)y(m)方向角α边长D(m)00.0000.00000°00′00″0.0006.88410.6951.6001326266.8844.20028.3335.4673316039.9664.20139.4459.51845131413.4094.200410.00913.68053483216.9504.200510.00717.88060455520.4904.20069.45222.04366472623.9843按坐标反算计算由O点至诸特征点的方向角、边长及间距,计算结果列于表中右边三栏。因定位时O、A间不通视,故在O点安置经纬仪,以B点定向,配置水平度盘读数90°00′00″。旋转照准部,待水平度盘读数为66°47′26″时,由O点起沿视线方向放样水平距离23.984m,标定6点。再旋转照准部,当水平度盘读数为60°45′55″时,沿视线方向放样05=20.490m,标定5点。实测56,其值与设计值4.200m的相对精度应符合要求,以资检核。依次放样诸特征点。4直角坐标法当圆心在建筑区以外较远时,宜计算特征点坐标,用直角坐标法定位。如图4a,建筑设计呈弧形,内弧半径R为76m,每间内弦长8m,进深12m,共8间。现以右半侧内弧轴线角点为例介绍其放样。图4如图4b,每间弦长所对的圆心角φ=2arcsin=6°02′02″取05方向为x轴,则特征点4的坐标x4=R*cosφ=75.579my4=R*sinφ=7.989m4因弧15(所对的圆心角φ1=4φ=24°08′08″故特征点1的坐标x1=R*cosφ1=69.356my1=R*sinφ1=31.076m同理计算其余各特征点的坐标。定位时,首先根据规划设计条件放样弧的两端点1与9,并标定弦的中点O1。实测边长,其值与设计值y1的相对精度应符合要求。然后,在O1点安置经纬仪,以点1或9定向,放样90°,沿视准轴方向分别放样水平距离=R-x1、=x2-x1、=x3-x1、……,依次标定5、O2、O3、……诸点。最后,分别在O2、O3、……点安置经纬仪,放样垂距y2、y3、……,依次标定2、3、……诸特征点。5切线支距法如图5,建筑设计呈弧形,位于临街转角处,外弧半径R为30.558m、弧长48m,进深12m,共6间。由于工字形楼宇使内、外弧之弦线方向均不能通视,所以不能采用上述方法定位。图5切线支距法是以弧线的起点或终点为坐标原点,切线方向为x轴,过原点的半径方向为y轴,根据坐标xi、yi按直角坐标5法放样诸特征点。现以放样外弧轴线角点为例介绍之。设角点i至起点(或终点)间的弧长为Si,弧长所对的圆心角为φi,则i点的坐标为(4)计算得:相邻两轴线的圆心角φ=15°,x1=7.909m、y1=1.041m,x2=15.279m、y2=4.094m,……定位时,可分别从弧的起点和终点向中点各放样弧线之半。首先,按规划设计条件放样弧的起点O、终点6,以及切线的交点A或圆心B。然后,沿切线方向放样水平距离x1\,x2\,……,标定垂足Ⅰ、Ⅱ、……。最后,在垂足Ⅰ、Ⅱ、……处分别放样垂距y1、y2、……,标定1、2、……诸特征点。6偏角法当弧的半径较大,弧线较长时,宜采用此法。如图6a...