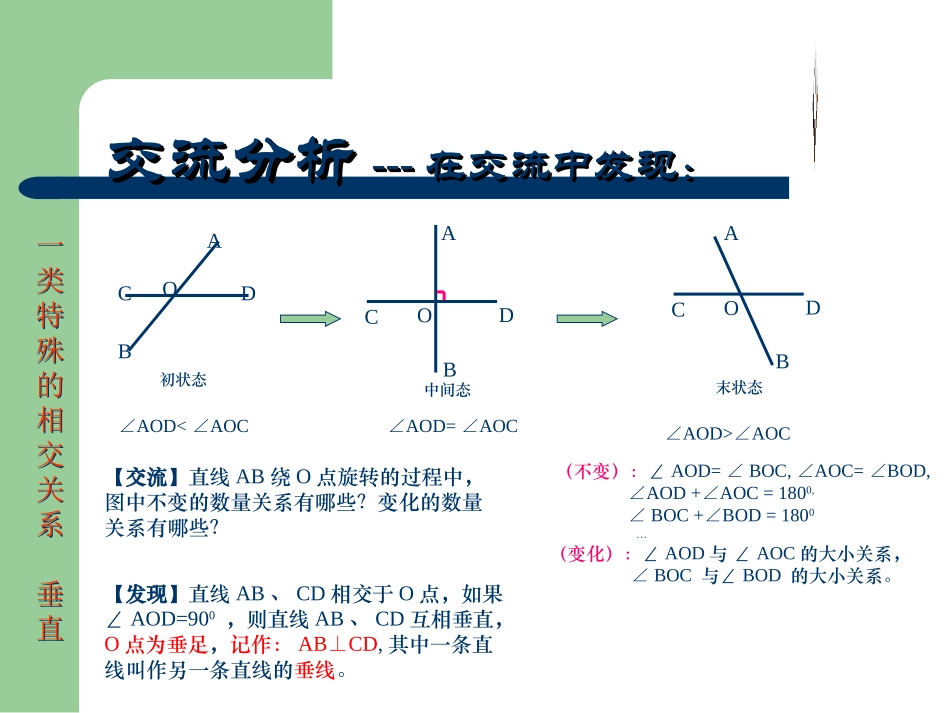
一类特殊的相交关系垂直一类特殊的相交关系垂直情景引入情景引入------在观察中感受:在观察中感受:情景引入情景引入------在观察中感受:在观察中感受:一类特殊的相交关系垂直一类特殊的相交关系垂直交流分析交流分析------在交流中发现:在交流中发现:交流分析交流分析------在交流中发现:在交流中发现:ABCDO中间态ABCDO初状态ABCDO末状态【交流】直线AB绕O点旋转的过程中,图中不变的数量关系有哪些?变化的数量关系有哪些?(不变):∠AOD=BOC,AOC=BOD,∠∠∠∠AOD+AOC=180∠0,∠BOC+BOD=180∠0…(变化):∠AOD与∠AOC的大小关系,∠BOC与∠BOD的大小关系。∠AOD
AOC∠【发现】直线AB、CD相交于O点,如果∠AOD=900,则直线AB、CD互相垂直,O点为垂足,记作:AB⊥CD,其中一条直线叫作另一条直线的垂线。一类特殊的相交关系垂直一类特殊的相交关系垂直垂线的定义有以下两层含义:ABCD1ABCD11:ABCD∵⊥(已知)∴∠1=90°(垂线的定义)2:1=90°∵∠(已知)∴ABCD⊥(垂线的定义)一类特殊的相交关系垂直一类特殊的相交关系垂直生活中的垂直生活中的垂直一类特殊的相交关系垂直一类特殊的相交关系垂直活动探究活动探究------在实践中收获:在实践中收获:活动探究活动探究------在实践中收获:在实践中收获:【思考】如何过一点画已知直线的垂线?o收获1:过直线外一点有且只有一条直线与已知直线垂直。讨论:点与直线的位置关系。【操作1】过直线外一点画已知直线的垂线?如右图动手画一画:一类特殊的相交关系垂直一类特殊的相交关系垂直活动探究活动探究------在实践中收获:在实践中收获:活动探究活动探究------在实践中收获:在实践中收获:o【操作2】过直线上一点画已知直线的垂线?如右图收获2:过直线上一点有且只有一条直线与已知直线垂直。【总结】过一点(已知直线上或已知直线外)有且只有一条直线与已知直线垂直。你能通过折纸解决以上问题吗?画出下列线段、射线的垂线。ABPQOA注意注意::画线段画线段((或射线或射线))的垂线时的垂线时,,有有时要将线段延长时要将线段延长((或将射线反向延长或将射线反向延长))后再画垂线后再画垂线..OM例例11、(、(11))如图,如图,分别过分别过AA、、BB、、CC作作BCBC、、ACAC、、ABAB的垂线。的垂线。AABBCC((22)、)、如图,过如图,过PP作直线作直线PM⊥OAPM⊥OA,垂足,垂足为点为点MM.过.过PP作线段作线段PN⊥OBPN⊥OB于于NN点。点。OOAABBPPDDEEFFMMNN一类特殊的相交关系垂直一类特殊的相交关系垂直例题解读例题解读------在应用中提升:在应用中提升:例题解读例题解读------在应用中提升:在应用中提升:解:∵∠1=35°,∠2=55°(已知)垂直(OEAB⊥)∴∠AOE=180°-∠1-∠2=180°-35°-55°=90°∴OEAB(⊥垂直的定义)例2:如图,已知直线AB、CD都经过O点,OE为射线,若∠1=35°2∠=55°,则OE与AB的位置关系是________________CDABOE12一类特殊的相交关系垂直一类特殊的相交关系垂直例题解读例题解读------在应用中提升:在应用中提升:例题解读例题解读------在应用中提升:在应用中提升:例3:如图,已知AB.CD相交于O,OECD⊥于O,AOC=36°∠,则∠BOE=。(A)36°(B)64°(C)144°(D)54°ABOCDE54°1.连接直线外一点与直线上各点的所有线段中,垂线段最短。垂线段最短2.直线外一点到这条直线的垂线段的长度,叫做点到直线的距离点到直线的距离。垂线段的长度简单说成:简单说成:垂线段最短.垂线段最短.思考:“垂线”与“垂线段”有什么区别?一类特殊的相交关系垂直一类特殊的相交关系垂直拓展应用拓展应用11有人不慎掉入有鳄鱼的湖中。如图,他在P点,应选择怎样的路线才能尽快游到岸边m呢?一类特殊的相交关系垂直一类特殊的相交关系垂直拓展应用拓展应用22如图:在铁路旁边有一张如图:在铁路旁边有一张庄,现在要建一火车站,庄,现在要建一火车站,为了使张庄人乘火车最方为了使张庄人乘火车最方便(即距离最近),请你便(即距离最近),请你在铁路上选一点来建火车在铁路上选一点来建火车站,并说明理由。站,并说明理由。张庄张庄∟∟垂线段最短立定跳远中,体育老师是如何测量运动员的成绩的?体育老师实际上测量的是点到直线的距离起跳线落脚点一类特殊的相交关系垂直一类特殊的相交关系垂直小结