实数（第一课时）VIP免费

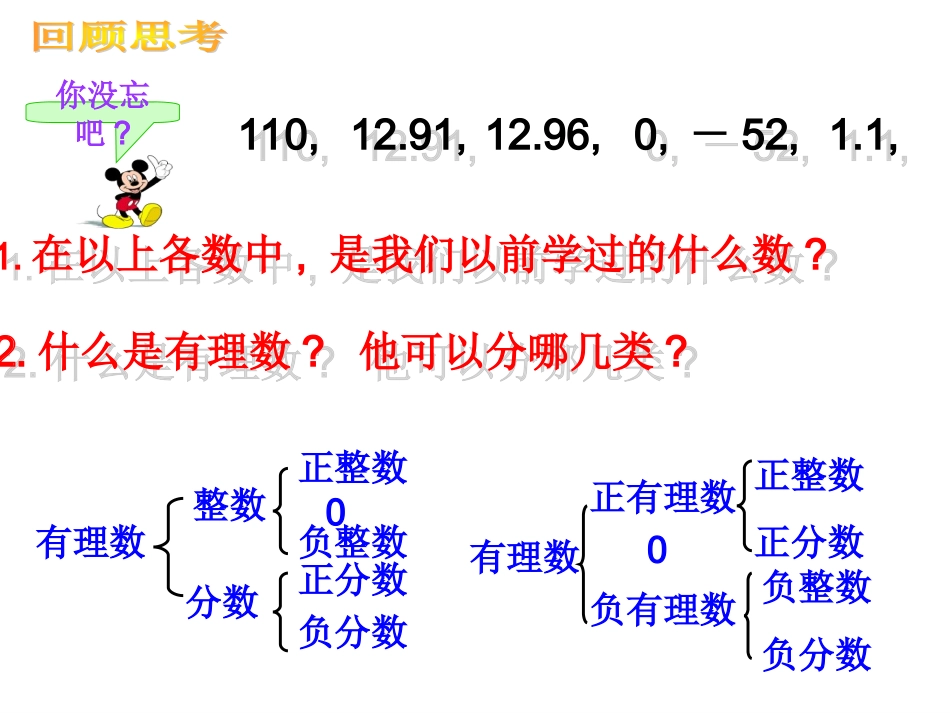
yunxanjiaoyu人教课标版八年级上册Gph郧县实验中学郧县实验中学黄建军黄建军报道二：在女子柔道－52公斤级的冠军争夺赛中,中国选手冼东妹仅用1.1分钟,就为中国柔道队夺得首枚金牌.报道二：在女子柔道－52公斤级的冠军争夺赛中,中国选手冼东妹仅用1.1分钟,就为中国柔道队夺得首枚金牌.报道一：在男子110米栏决赛中，中国选手刘翔以12.91秒的成绩夺得金牌,这个成绩打破12.96的奥运会纪录,平了世界纪录,实现了中国男子田径金牌0的突破.报道一：在男子110米栏决赛中，中国选手刘翔以12.91秒的成绩夺得金牌,这个成绩打破12.96的奥运会纪录,平了世界纪录,实现了中国男子田径金牌0的突破.有理数正有理数负有理数0你没忘吧?有理数正分数正整数负整数负分数分数整数正整数0负整数正分数负分数12.96,110,110,12.91,12.91,1.1,1.1,－52,－52,0,0,1.在以上各数中,是我们以前学过的什么数?1.在以上各数中,是我们以前学过的什么数?2.什么是有理数?他可以分哪几类?2.什么是有理数?他可以分哪几类?使用计算器计算,把下列各数写成小数的形式，你有什么发现？95,9011,119,847,53,35.095,21.09011,81.0119,875.5847,6.053,0.33事实上，任何一个有理数都可以写成有限小数或无限循环小数。设x=0.3=0.333…①则１０x＝３．３３３…②则②－①得９x=3,即x=1\3根据上面提供的方法，你能把5.875,0.81化成分数吗？且想一想是不是任何有限小数或无限循环小数都可以化成分数？......反过来，任何有限小数或无限循环小数也都是有理数,11981.0,847875.5除了有限小数和无限循环小数，还有什么其它类型的小数吗？无限不循环的小数----------叫做无理数无理数也像有理数一样广泛存在着。3无理数也有正负之分，例如正无理数：负无理数：—2—23—无理数有那些特征呢？12,2,２．开不尽方的数例如：例如：12,3,7注意:带根号的数不一定是无理数３．有一定的规律，但不循环的无限小数—168.3232232223…〔两个3之间依次多1个2〕0.1010010001…〔两个1之间依次多1个0〕0.1010010001…〔两个1之间依次多1个0〕0.12345678910111213…〔小数部分有相继的正整数组成〕0.12345678910111213…〔小数部分有相继的正整数组成〕１．圆周率及一些含有的数１．圆周率及一些含有的数１．圆周率及一些含有的数１．圆周率及一些含有的数１．圆周率及一些含有的数１．圆周率及一些含有的数１．圆周率及一些含有的数１．圆周率及一些含有的数１．圆周率及一些含有的数１．圆周率及一些含有的数,41把下列各数分别填入相应的集合内：,23,7,,25,2,320,5,83,94,03737737773.0（相邻两个3之间的7的个数逐次加1）有理数集合无理数集合,83,41,25,94,0,23,7,,2,320,53737737773.0有理数和无理数统称有理数和无理数统称实数实数..有理数和无理数统称有理数和无理数统称实数实数..负无理数正无理数负有理数正有理数零有理数无理数实数由上可知:1.实数可分为哪两类数?由上可知:1.实数可分为哪两类数?探究实数的分类(一)2.有理数可分为哪几类?2.有理数可分为哪几类?3.无理数可分为哪几类?3.无理数可分为哪几类?负无理数正无理数负有理数正有理数零有理数无理数实数负无理数正无理数负有理数正有理数零有理数无理数实数⑧①②③④⑤⑥⑦依据实数的分类（一）示意图,在右图的卡片上填上下列数的名称.依据实数的分类（一）示意图,在右图的卡片上填上下列数的名称.正有理数正有理数零零负有理数负有理数正无理数正无理数负无理数负无理数有理数有理数无理数无理数实数实数负无理数正无理数负有理数正有理数零有理数无理数实数探究实数的分类(二)正有理数正有理数正无理数正无理数负有理数负有理数负无理数负无理数正实数正实数00负实数负实数实数实数依据实数的分类（二）示意图,在右图的卡片上填上下列数的名称.依据实数的分类（二）示意图,在右图的卡片上填上下列数的名称.①①②②实数实数③③④④⑤⑤⑥⑥⑦⑦⑧⑧正实数正实数零零负实数负实数正有理数正有理数正无理数正无理数负有理数负有理数负无理数负无理数你学会了吗?把下列各数填...