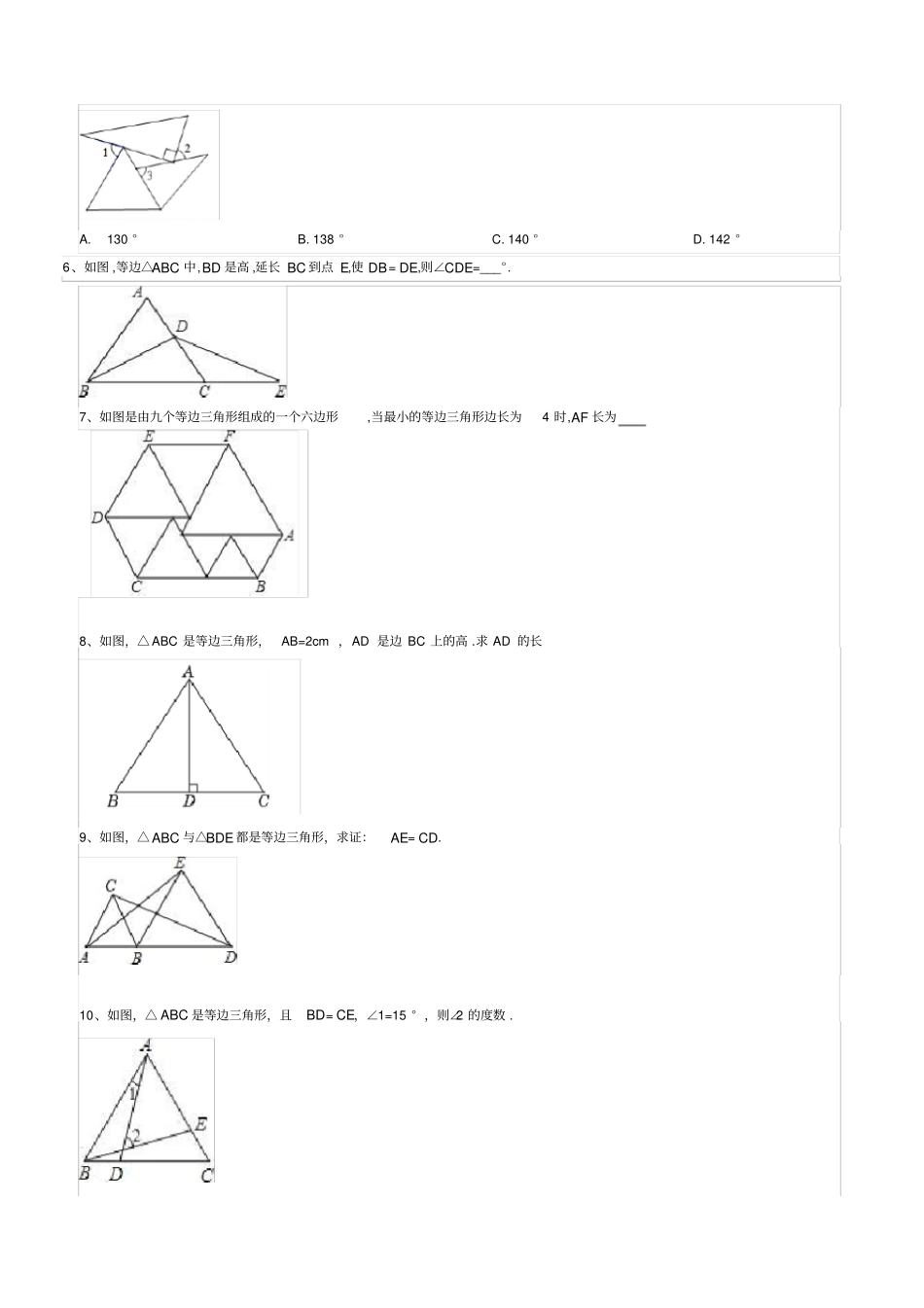
等腰三角形性质的应用及性质和等边三角形的性质题型一、利用等腰三角形中的相等线段求解1、如图,在△ABC中,AB=AC,BD是角平分线,若∠BDC=69°,则∠A等于()A.32°B.36°C.48°D.52°2、在△ABC中,AB=AC,下列条件中,不能使BD=CE的是()A.BD,CE分别为AC,AB上的高B.BD,CE为∠ABC,∠ACB的角平分线C.∠ABD=31∠ABC,∠ACE=31∠ACBD.∠ABD=∠BCE3、如图,在△ABC中,AB=AC,D为BC上的一点,DE⊥AB于E,DF⊥AC于F,BM为AC边上的高,试探索DE+DF与BM的大小关系。题型二、利用等边三角形的性质求解4、如图,△ABC是等边三角形,BD⊥AC于D,若AB=4,则AD的长为()A.1B.1.5C.2D.2.55、一个等边三角形,一个直角三角形以及一个等腰三角形如图放置,已知等腰三角形的底角∠3=72°,则∠1+∠2____。A.130°B.138°C.140°D.142°6、如图,等边△ABC中,BD是高,延长BC到点E,使DB=DE,则∠CDE=___°.7、如图是由九个等边三角形组成的一个六边形,当最小的等边三角形边长为4时,AF长为8、如图,△ABC是等边三角形,AB=2cm,AD是边BC上的高.求AD的长9、如图,△ABC与△BDE都是等边三角形,求证:AE=CD.10、如图,△ABC是等边三角形,且BD=CE,∠1=15°,则∠2的度数.等腰三角形的性质与判定的应用题型一、等腰三角形的角度问题1、在等腰三角形一底角为50°,则顶角的度数是()A.65°B.70°C.75°D.80°2、等腰三角形的一个内角是100°,则这个三角形的底角的大小是()A.35°B.40°C.45°D.48°3、已知:△ABC中,AB=AC,∠B-∠A=30°,则∠A=___.4、已知等腰三角形的一个内角为50°,则顶角的度数为_____.题型二、等腰三角形的边长问题5、如果等腰三角形的周长为10,一边长为3,那么这个等腰三角形的另两条边长为___.6、等腰三角形的三边长分别为:x+1,2x+3,9,则x=______.7、已知等腰三角形的周长为18cm,其中两边之差为6cm,求三角形的各边长。题型三、等腰三角形“三线合一”问题8、等腰三角形一腰上的高与另一腰所成的夹角为45°,则这个等腰三角形的顶角的度数为______.9、等腰三角形一腰上的中线将这个等腰三角形的周长分成15cm和6cm两部分。求等腰三角形的底边长。题型四、等腰三角形的性质与判定综合应用10、如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,下列结论错误的是()A.∠C=2∠AB.BD=BCC.△ABD是等腰三角形D.点D为线段AC的中点11、如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN//BC交AB于M,交AC于N,若△AMN的周长为18,BC=6,则△ABC的周长为12、如图,在△ABC中,AB=AC,点D.E.F分别在BC、AB、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)当∠A=40°时,求∠DEF的度数。