反比例函数复习课精选VIP免费

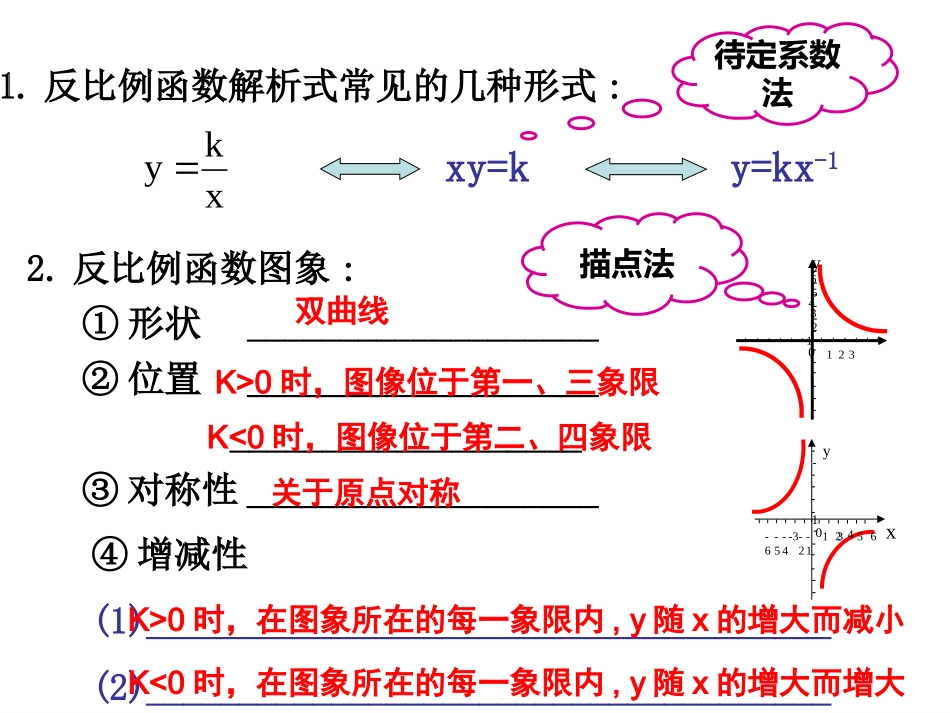
反比例函数复习反比例函数复习y0123123456-40-51-3yx2345-16-2-612.反比例函数图象:①形状___________________②位置______________________________________③对称性___________________④增减性(1)_____________________________________(2)_____________________________________1.反比例函数解析式常见的几种形式:双曲线K>0时，图像位于第一、三象限K<0时，在图象所在的每一象限内,y随x的增大而增大K<0时，图像位于第二、四象限K>0时，在图象所在的每一象限内,y随x的增大而减小关于原点对称xkyy=kx-1xy=k待定系数法描点法已知1221mxmy如果y是x的正比例函数，m=_____-1如果y是x的反比例函数，m=_____01.已知y-1与x+2成反比例，当x=2时,y=9。请写出y的x函数关系。2.若y=y1-y2,其中y1与x2成反比例,其中y2与x成反比例,且当x=1时,y=3;当x=-1时,y=7。求当x=2时,y的值为多少?思考题：(2007成都市中考题)如图，一次函数y=kx+b的图象与反比例函数的图象交于A(-2,1),B(1,n)两点．（1）试确定上述反比例函数和一次函数的表达式；（2）求⊿AOB的面积．myxOyxBACD例：第二板块：基本题型复习-40-51-3yx2345-16-2-61y1y2y3321yyyy0xBA题型二D解题要点：正、反比例函数图像的交点关于原点对称。x0yAB23xy6ABCEOFxyx(2007武汉市)如图，已知双曲线(x＞0)经过矩形OABC边AB的中点F，交BC于点E，且四边形OEBF的面积为2，则k＝____。xky2SAOF⊿=S矩形AOCB41SAOF⊿=S四边形EOBF=121OACD例：思索归纳题型三BKS21三角形kyxS矩形yx0PACDEFAPOPSAOP21△xyyx2121k211.将几何图形的边长用表示,xy2.利用K=x·y将图形的面积化成含的代数式kxy4),(yx,xy),(yx,xy),(yx解题要点:形如下图中图形的面积KS矩形变3:如图，A、C是函数的图象上关于原点O对称的任意两点，过C向x轴引垂线，垂足为B，则三角形ABC的面积为。xy2考察面积不变性和中心对称性。2如图、一次函数y1=x-2的图象和反比例函数的图象交于A(3,1)、B(n,-3)两点.(1)求k、n的值。(2)x取何值时,y1y﹥2。AB_kxy2=yxoy1=x-2_3xy2=(1)k=3,n=-1,(2)当x3﹥或-1x0﹤﹤时,y1y﹥2。1C-13题型四第三板块：生活情境题——反比例函数的应用解：(1)设函数关系式为y=k/(x-0.4),又当x=0.65元时，y=0.8,则有0.8=k/(0.65-0.4),解得k=0.2.∴y与x之间的函数关系式为y=0.2/(x-0.4),即。某地上年度电价为0.8元，年用电量为1亿度，本年度计划将电价调至0.55～0.75元之间，经测算，若电价调至x元，则本年度新增用电量y(亿度)与(x－0.4)元成反比例．又当x＝0.65元时，y＝0.8．(1)求y与x之间的函数关系式；(2)若每度电的成本价0.3元，电价调至0.6元，请你预算一下本年度电力部门的纯收人多少?251xy(2)把x=0.6代入y=0.2/(x-0.4)，得y=1.即本年度新增用电量1亿度则本年度总用电量为（1+1=2）亿度∴本年度电力部门的纯收入为：2×（0.6-0.3)=0.6亿元。为了预防“流感”,某学校对教室采用药熏消毒法进行毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请根据题中所提供的信息,解答下列问题:(1)药物燃烧时,y关于x的函数关系式为:________,自变量x的取值范围是:_______,药物燃烧后y关于x的函数关系式为_______.(2)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?6O8x(min)y(mg)学以致用为了预防“流感”,某学校对教室采用药熏消毒法进行毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请根据题中所提供的信息,解答下列问题:(1)药物燃烧时,y关于x的函数关系式为:________,自变量x的取值范围是:__________,药物燃烧后y关于x的函数关系式为_____________.6O8x(min)y(mg)学以致用)0(kkxy式为根据图像，设函数解析x43y68）代入，求出，将点（)0(kxky式为根据图像，设函数解析)8(48y68xx）代入，求...