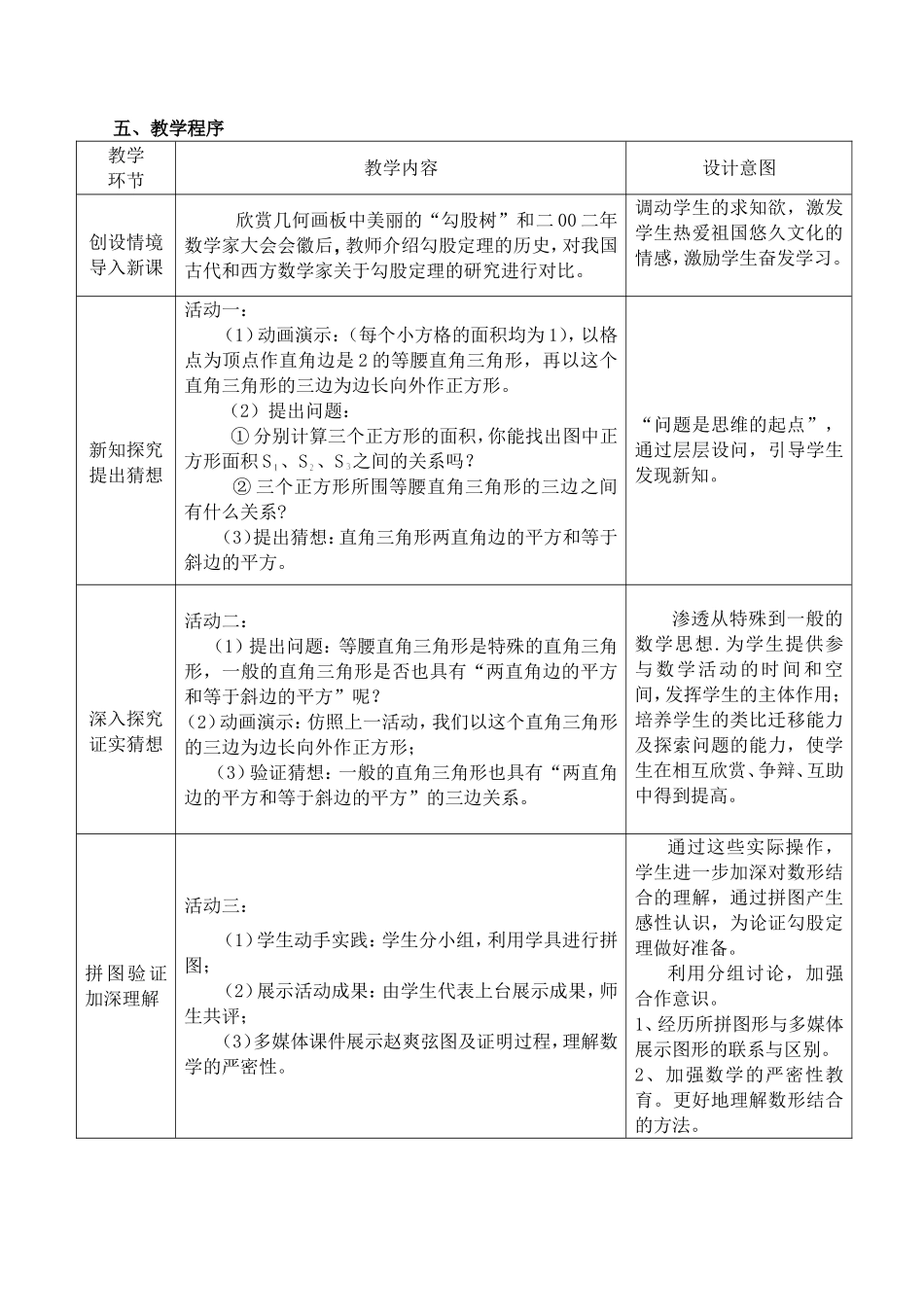
18.1《勾股定理》第一课时教学设计汉川市庙头中学张丽红一、教学背景1、面向学生:八年级2、学科:数学3、课时:1课时4、课前准备:勾股定理相关内容、课件和图片5、学情分析:在学习了一般三角形的有关性质后,进一步学习特殊三角形的性质-—直角三角形三边的关系。二、教学课题:1、通过对比国内外数学家对勾股定理的研究成果,对学生进行爱国主义教育和民族精神的培养。2.、用数形结合这一重要的数学思想来证明勾股定理,提高学生的解题技能。三、教材分析(一)教材的地位与作用勾股定理是数学中几个重要定理之一,也是我国古代数学家智慧的结晶。它揭示的是直角三角形中三边的数量关系。它在数学的发展中起着重要的作用,在现实世界中也有着广泛的应用。学生通过对勾股定理的学习,可以在原有的基础上对直角三角形有进一步的认识和理解。(二)教学目标知识与技能:1、了解勾股定理的文化背景,体验勾股定理的探索过程,掌握勾股定理的验证方法。2、了解勾股定理的内容。3、能利用已知两边的长求第三边的长。过程与方法:1、在勾股定理的探索过程中,培养合情推理能力,体会数形结合和从特殊到一般的思想。2、通过拼图活动,体验数学思维的严谨性,发展形象思维。3、在探索活动中,学会合作与交流。情感、态度与价值观:1、通过对比介绍我国古代和西方数学家关于勾股定理的研究,激发学生热爱祖国悠久文化的情感,激励学生奋发学习。2、在探索勾股定理的过程中,体验收获成功的快乐,锻炼克服困难的勇气,培养合作意识和探索创新精神。(三)教学重、难点重点:探索和证明勾股定理难点:用拼图方法证明勾股定理(四)学情分析学生对几何图形的观察,几何图形的分析能力已初步形成。部分学生解题思维能力比较强,能够正确归纳所学知识,通过学习小组讨论交流,能够形成解决问题的思路。现在的学生已经厌倦教师单独的说教方式,希望教师设计便于他们进行观察的几何环境,给他们自己探索、发表自己见解和展示自己才华的机会;更希望教师满足他们的创造愿望。四、教学策略本节课采用探究发现式教学,由浅入深,由特殊到一般地提出问题,鼓励学生采用观察分析、自主探索、合作交流的学习方法,让学生经历数学知识的形成与应用过程。五、教学程序教学环节教学内容设计意图创设情境导入新课欣赏几何画板中美丽的“勾股树”和二00二年数学家大会会徽后,教师介绍勾股定理的历史,对我国古代和西方数学家关于勾股定理的研究进行对比。调动学生的求知欲,激发学生热爱祖国悠久文化的情感,激励学生奋发学习。新知探究提出猜想活动一:(1)动画演示:(每个小方格的面积均为1),以格点为顶点作直角边是2的等腰直角三角形,再以这个直角三角形的三边为边长向外作正方形。(2)提出问题:①分别计算三个正方形的面积,你能找出图中正方形面积S、S、S之间的关系吗?②三个正方形所围等腰直角三角形的三边之间有什么关系?(3)提出猜想:直角三角形两直角边的平方和等于斜边的平方。“问题是思维的起点”,通过层层设问,引导学生发现新知。深入探究证实猜想活动二:(1)提出问题:等腰直角三角形是特殊的直角三角形,一般的直角三角形是否也具有“两直角边的平方和等于斜边的平方”呢?(2)动画演示:仿照上一活动,我们以这个直角三角形的三边为边长向外作正方形;(3)验证猜想:一般的直角三角形也具有“两直角边的平方和等于斜边的平方”的三边关系。渗透从特殊到一般的数学思想.为学生提供参与数学活动的时间和空间,发挥学生的主体作用;培养学生的类比迁移能力及探索问题的能力,使学生在相互欣赏、争辩、互助中得到提高。拼图验证加深理解活动三:(1)学生动手实践:学生分小组,利用学具进行拼图;(2)展示活动成果:由学生代表上台展示成果,师生共评;(3)多媒体课件展示赵爽弦图及证明过程,理解数学的严密性。通过这些实际操作,学生进一步加深对数形结合的理解,通过拼图产生感性认识,为论证勾股定理做好准备。利用分组讨论,加强合作意识。1、经历所拼图形与多媒体展示图形的联系与区别。2、加强数学的严密性教育。更好地理解数形结合的方法。abc归纳定理变式应用勾...