圆周角课件黄鹤VIP免费

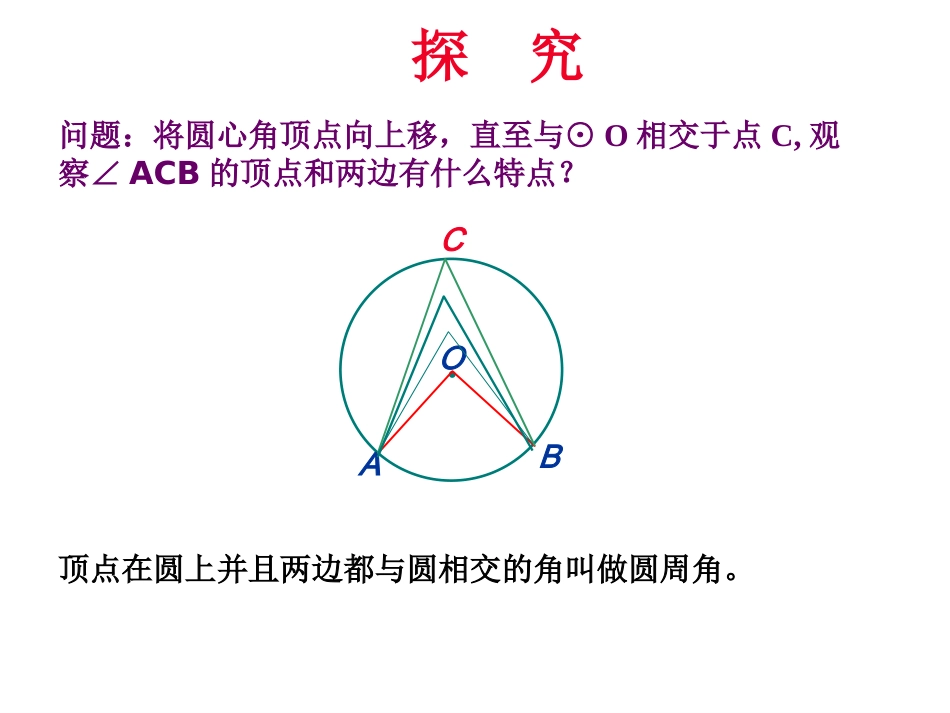
24.1.4圆周角仁怀市育人中学---黄鹤温故而知新1.什么叫圆心角?.OAB顶点在圆心的角叫圆心角探究.OA问题：将圆心角顶点向上移，直至与⊙O相交于点C,观察∠ACB的顶点和两边有什么特点？C顶点在圆上并且两边都与圆相交的角叫做圆周角。B理解圆周角的概念？下列各图中的∠APB是否是圆周角？o(p)BOBPOAOPABOBOAOBOPAAPBAPPBAPAB观察思考？如图是一个圆柱形的海洋馆的横截面示意图,人们可以通过其中的圆弧形玻璃窗AB观看窗内的海洋动物,同学甲站在圆心O的位置，同学乙站在正对着玻璃窗的靠墙的位置C，他们的视角(AOB∠和∠ACB)有什么关系?如果同学丙、丁分别站在其他靠墙的位置D和E，他们的视角（∠ADB和∠AEB）和同学乙的视角（∠ACB）相同吗？︵探究①分别量一下所对的圆周角∠ACB、∠ADB、∠AEB的度数比较一下，再改变圆周角的位置，圆周角的度数有没有变化？你有什么发现？②再量出图中所对的圆周角和圆心角的度数，比较一下，你有什么发现？ABABOBACDE验证:为了验证我们的猜想，我们根据圆周角与圆心的相对位置关系分三种情况来证明：（1）圆心在圆周角的一边上；（2）圆心在圆周角的内部；（3）圆心在圆周角的外部OBAPOBAPOPB第一种情况：ABCO∵OA=OC∴∠A=C∠又∠BOC=A∠＋∠C∴∠BOC=2A∠∠即A=BOC∠21ABCOD证明：由第1种情况得∠即BAC=BOC∠21∠BAD＝∠BOD21∠CAD＝∠COD21∠BAD＋∠CAD＝∠BOD＋∠COD2121第二种情况：ABCO3.第三种情况：请同学们课后合作完成？·ABC1OC2C3在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．圆周角定理推论一：1、半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．·ABCDEO推论二：2、在同圆或等圆中，如果两个圆周角相等，它们所对的弧也相等。观察思考？如图是一个圆柱形的海洋馆的横截面示意图,人们可以通过其中的圆弧形玻璃窗AB观看窗内的海洋动物,同学甲站在圆心O的位置，同学乙站在正对着玻璃窗的靠墙的位置C，他们的视角(AOB∠和∠ACB)有什么关系?如果同学丙、丁分别站在其他靠墙的位置D和E，他们的视角（∠ADB和∠AEB）和同学乙的视角（∠ACB）相同吗？︵1.如图，点A、B、C、D在同一个圆上，四边形ABCD的对角线把4个内角分成8个角，这些角中哪些是相等的角？ABCD12345678练习一3、如图，AB是⊙O的直径，∠AOD是圆心角，∠BCD是圆周角，若∠BCD=25°，则∠AOD=。OABCD130°练习二例2如图，⊙O直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC、AD、BD的长．86102222ACABBC又在Rt△ABD中，AD2+BD2=AB2，221052(cm)22ADBDAB·ABCDO解：∵AB是直径，∴∠ACB=∠ADB=90°．在Rt△ABC中，∵CD平分∠ACB，练习三（请同学们合作完成，书写过程要规范整洁）106））8∴∠ACD=∠BCD∴AD=BD∴AD=BD︵︵说出你这节课的收获和体验，让大家与你一起分享吧！作业：1、请证明课堂上未完成的第三种情况？2、P85.左边方框里面要求的证明？3、P87.第4小题3.求证：如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形．（提示：作出以这条边为直径的圆.）·ABCO已知：△ABC，CO为AB边上的中线，求证：△ABC为直角三角形.证明：以AB为直径作⊙O，∵AO=BO，∴AO=BO=CO.∴点C在⊙O上.∵AB为直径,12且CO=AB∴△ABC为直角三角形.∴∠ACB=90°．12且CO=AB1、如图，在⊙O中，AB为直径，CB=CF,弦CGAB⊥，交AB于D，交BF于E求证：BE=EC⌒⌒⌒⌒证明：连接AO并延长交⊙O于D。由第1种情况得∠即BAC=BOC∠21∠BAD＝∠BOD21∠CAD＝∠COD21∠CAD－∠BAD＝∠COD－∠BOD2121ABCOD3.第三种情况：