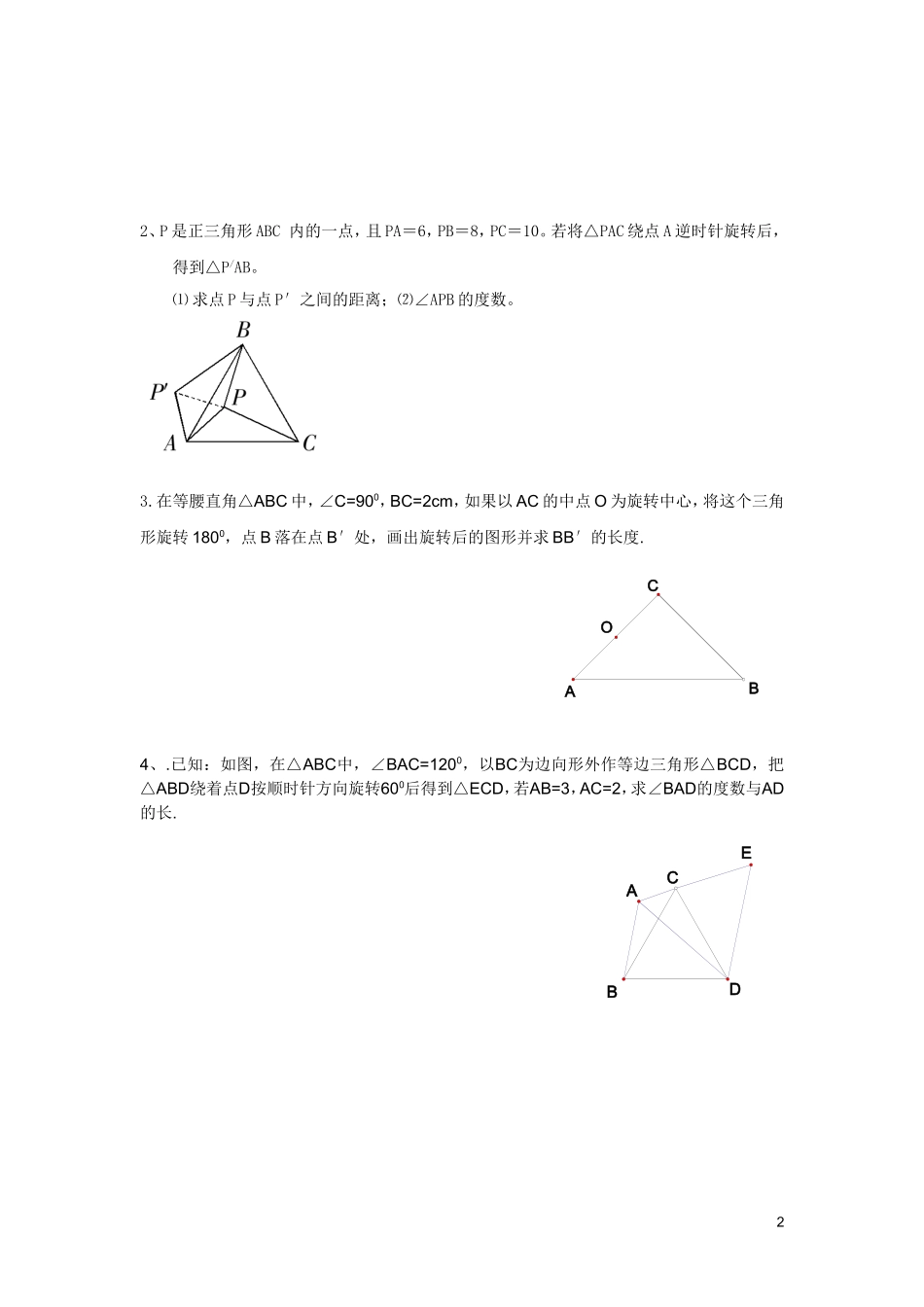
《图形的旋转》应用例:如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示)小明在对这两张三角形纸片进行如下操作时遇到了两个问题,请你帮助解决.(图1)(图2)(图3)(图1)(图2)(图3)(图4)(图5)(1)将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F重合,请你求出平移的距离;(2)将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度.分析:这是一道操作型的计算题.分别考察了平移和旋转变换中有关量的变化规律,还涉及到含30°角的直角三角形的计算.解决这类问题首先要正确画出变换后的对应图形,确定变化规律,再分析求解.解:(1)图形平移的距离就是线段BC(即BF)的长.又∵在Rt△ABC中,斜边长为10cm,∠BAC=30,∴BC=5cm,∴平移的距离为5cm.(2)∵∠1AFA=30°,∴∠60GFD,∠D=30°.∴∠90FGD.在Rt△EFD中,ED=10cm,∴FD=53,∴532FGcm.练习:1、如图,四边形ABCD中,∠BAD=∠C=90º,AB=AD,AE⊥BC于E,若线段AE=5,求ABCDS四边形.(提示:将△ABE绕点A旋转90º,使AB与AD重合.将四边形ABCD割补为正方形)1EDCBA2、P是正三角形ABC内的一点,且PA=6,PB=8,PC=10。若将△PAC绕点A逆时针旋转后,得到△P/AB。⑴求点P与点P′之间的距离;⑵∠APB的度数。3.在等腰直角△ABC中,∠C=900,BC=2cm,如果以AC的中点O为旋转中心,将这个三角形旋转1800,点B落在点B′处,画出旋转后的图形并求BB′的长度.4、.已知:如图,在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长.2OBCACBDAE