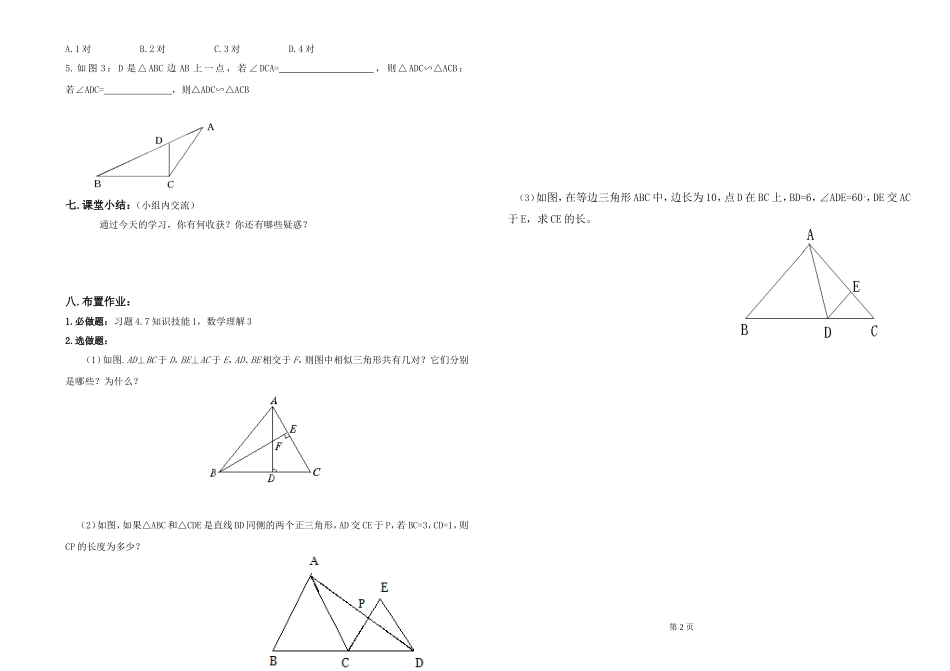
4.6.探索三角形相似的条件(第一课时)一.学习目标:1.经历两个三角形相似条件的探索过程,进一步发展学生的探究、交流能力,以及动手、动脑、手脑和谐一致的习惯。2.初步掌握根据两个角对应相等来判定两个三角形相似的方法。3.能够运用三角形相似的条件解决简单的问题,进一步发展学生的合情推理能力和初步的逻辑推理意识。二.学习重点:相似三角形的判定定理1以及推导过程,并会用判定方法来证明和计算。三.学习难点:相似三角形的判定定理1的应用。四.课前导学:1.什么是相似三角形?什么是相似比?2.△ABC∽△DEF,相似比为2,已知AB=1,AC=2,∠A=90°,则△DEF是周长是_________.3.△ABC的三条边长之比为2:5:6,与其相似的另一个△A′B′C′的最大边为18厘米,那么△ABC最小边是_________,另一边是________.4.证明两个三角形全等的方法有:,此外还有证明两个直角三角形全等的.5.下列说法中,不正确的是()A.两个全等的三角形相似B.两个相似三角形全等C.若两个相似三角形的相似比为1则这两个三角形全等D.若两个三角形都与第三个三角形相似,那么这两个三角形相似6.△ABC∽△A′B′C′,若BC=6,B′C′=9,则△A′B′C′与△ABC的相似比为()A:5:3B:3:2C:2:3D:3:5五.思维结合,精髓展示:1.每人画一个△ABC,使得∠BAC=60°,与同伴交流,你们所画的三角形相似吗?2.与同伴合作,一人画△ABC,另一人画△A′B′C′,使得∠A和∠A′都等于50°,∠B和∠B′都等于60°,比较你们画的两个三角形,∠C与∠C′相等吗?对应边的比相等吗?这样的两个三角形相似吗?改变两个角的大小,再试一试.由此可得出三角形相似的判定方法一:.简称.3.如图,D、E分别是△ABC边AB、AC上的点,DE∥BC(1)图中有哪些相等的角?(2)找出图中的相似三角形,并说明理由;(3)写出三组成比例的线段(4)在上面的条件下,吗?六.课堂效果检测:1.下列各图可能不相似的是()A.各有一个角是50°的两个等腰三角形B.各有一个角是60°的两个等腰三角形C.两个等腰直角三角形D.各有一个角是105°的两个等腰三角形2.如图1:锐角三角形ABC的高CD和BE相交于点O,则图中与△ODB相似的三角形的个数是()A.1B.2C.3D.4图1图23.如果一个三角形的一条高把这个三角形分为两个相似三角形,那么这个三角形必是()A.等腰三角形B.任意三角形C.直角三角形D.直角三角形或等腰三角形4.如图2:△ABC中,DE∥BC,EF∥AB,则图中有相似三角形()第1页第2页A.1对B.2对C.3对D.4对5.如图3:D是△ABC边AB上一点,若∠DCA=,则△ADC∽△ACB;若∠ADC=,则△ADC∽△ACB图3七.课堂小结:(小组内交流)通过今天的学习,你有何收获?你还有哪些疑惑?八.布置作业:1.必做题:习题4.7知识技能1,数学理解32.选做题:(1)如图.AD⊥BC于D,BE⊥AC于E,AD、BE相交于F,则图中相似三角形共有几对?它们分别是哪些?为什么?(2)如图,如果△ABC和△CDE是直线BD同侧的两个正三角形,AD交CE于P,若BC=3,CD=1,则CP的长度为多少?(3)如图,在等边三角形ABC中,边长为10,点D在BC上,BD=6,∠ADE=60。,DE交AC于E,求CE的长。第1页第2页