倾斜角与斜率1VIP免费

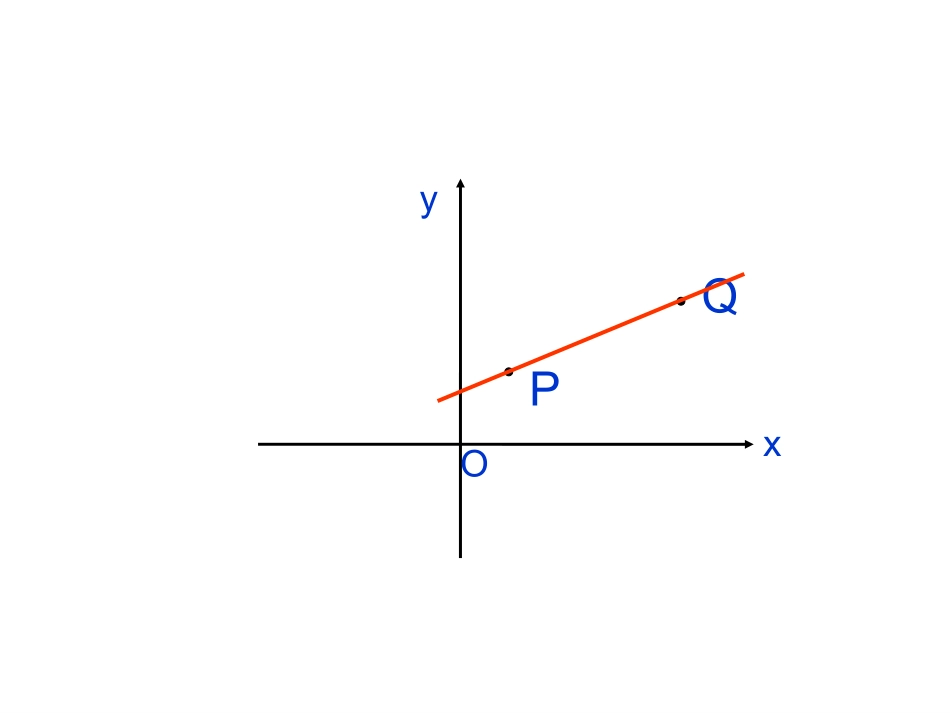
PQOyxOyxP1.正确理解直线的倾斜角和斜率的概念；（重点）2.理解直线的斜率的存在性；（难点）3.斜率公式的推导过程，掌握过两点的直线的斜率公式．（重点、难点）01/05/25OxyＰ一、直线的倾斜角当直线与x轴相交时，我们取x轴为基准，x轴正向与直线向上方向之间所形成的角叫做直线的倾斜角。lll；角为轴平行或重合时，倾斜规定：当直线与ox0)1(；的取值范围为倾斜角oo1800)2(loyxloyxlyoxloyxl直线倾斜角的意义体现了直线对x轴正方向的倾斜程度在平面直角坐标系中，每一条直线都有一个确定的倾斜角。倾斜角倾斜程度2l3lx1lyo倾斜角能确定一条直线吗？相同倾斜角可作无数互相平行的直线如何才能确定直线位置？yxola一点+倾斜角确定一条直线过一点且倾斜角为能不能确定一条直线？a（两者缺一不可）能日常生活中，还有没有表示倾斜程度的量？前进量升高量前进量升高量坡度（比）前进量升高量α“坡度比”是“倾斜角”的正切值.xyo二、直线斜率的定义通常用小写字母k表示，即ktan一条直线的倾斜角的正切值叫做这条直线的斜率xyoα倾斜角斜率0300450600009001200135015033133313不存在00(90)poyxlypoxlpoyxlpoyxl0°＜＜90°=90°00k=0k>0k不存在k<000090180探究：由两点确定的直线的斜率),(111yxP),(222yxP21PPQ如图，当α为锐角时，能不能构造一个直角三角形去求？tankxyo1x2x1y2y),(12yxQ中在QPPRt12QPQPQPPk1212tantan1212xxyy锐角xyo),(111yxP),(222yxP),(12yxQ如图，当α为钝角时，180tan)180tan(tan中在12QPPRtQPQP12tan2112xxyy12122112tanxxyyxxyyk1x2x1y2y钝角思考？xyo(3)),(12yxQ),(111yxP),(222yxPyox(4)),(12yxQ),(111yxP),(222yxP21pp1、当的位置对调时，值又如何呢？k2121tanyyxx说明：此公式与两点坐标的顺序无关.思考？2、当直线平行于x轴，或与x轴重合时，上述公式还适用吗？为什么？xyo),(111yxP),(222yxP1x2x1212xxyyk00tan0k答：成立，因为分子为0，分母不为0，K=03、当直线平行于y轴，或与y轴重合时，上述公式还适用吗？为什么？xyo),(111yxP),(222yxP1y2y1212xxyyk思考？不存在不存在k)(90tan,90答：不成立，因为分母为0。直线的斜率公式：综上所述，我们得到经过两点),,(111yxP)(21xx),(222yxP的直线斜率公式：)(21211212xxyykxxyyk或2P2P1P1P公式特点：(1)与两点坐标的顺序无关;(2)公式表明,直线的斜率可以通过直线上任意两点的坐标来表示,而不需要求出直线的倾斜角；(3)当x1=x2时,公式不适用,此时α=90°.例1如下图，已知A(3，2),B(-4，1),C（0，-1）,求直线AB，BC，CA的斜率，并判断这些直线的倾斜角是锐角还是钝角.OxyACB121;437ABk解：直线AB的斜率1121;0(4)42BCk直线BC的斜率直线CA的斜率1231.033CAk分析：直接利用公式求解例2在平面直角坐标系中，画出经过原点且斜率分别为1，-1，2及-3的直线l1，l2，l3及l4.xy解：设A1（x1,y1）是l1上任一点，根据斜率公式有:1101,0yx即x1=y1.设x1=1，则y1=1，于是A1的坐标是（1,1）．过原点及点A1（1,1）的直线即为l1．1l分析：找出直线异于原点的点.1AO同理l2是过原点及点A2（1，-1）的直线，l3是过原点及点A3（1，2）的直线，l4是过原点及点A4（1，-3）的直线．x1A1l3l2l4l2A4Ay3AOl11.直线倾斜角的定义及其范围：2.斜率k与倾斜角之间的关系：3.斜率公式：ktan(90)2121121212()yykxxyykxxxx0180作业本：P86页练习第3题、第4题课后练习：《世纪金榜》学业达标预习：怎样用斜率判断两直线平行与垂直？