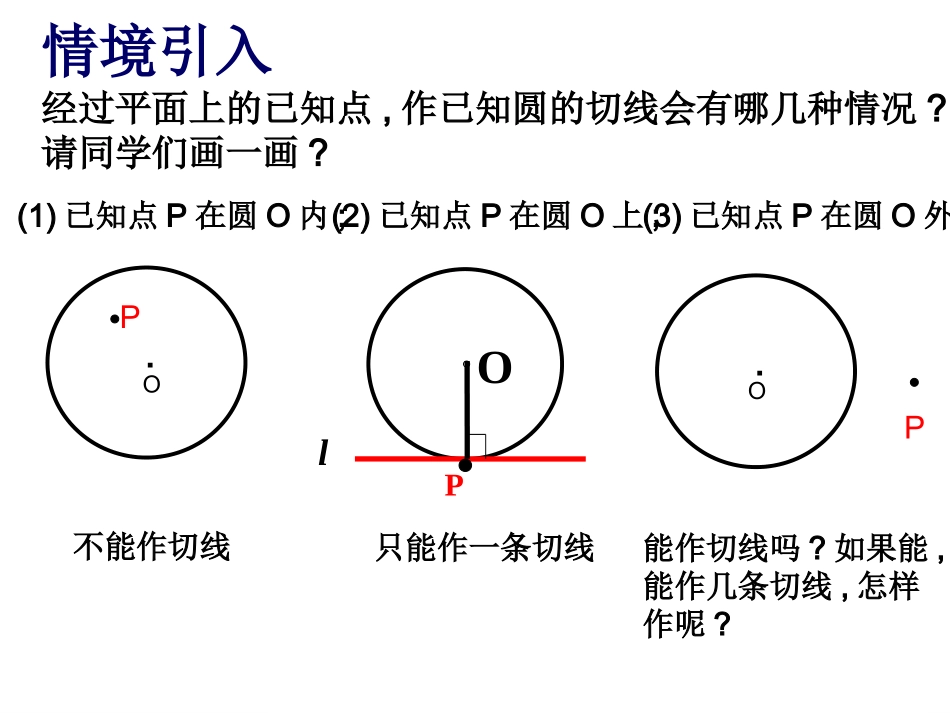
情境引入经过平面上的已知点,作已知圆的切线会有哪几种情况?请同学们画一画?(1)已知点P在圆O内;P.O(2)已知点P在圆O上;OlP(3)已知点P在圆O外.不能作切线只能作一条切线P.O能作切线吗?如果能,能作几条切线,怎样作呢?··oo′p1.连结OP2.以OP为直径作⊙O′,与⊙O交于A、B两点。AB请问(1)直线PA、PB是⊙O的切线吗?为什么?(2)点A,点B与直线PO有什么关系?为什么?(多种方法)如图,已知⊙O外一点P,你能用尺规过点P作⊙O的切线吗?由此你能得出什么结论?1.过圆外一点作圆的切线,可以作两条2.点A和点B关于直线OP对称合作探究合作探究观察下列作图过程3.作直线PA,PB经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长。·oABp切线长注意:切线与切线长的区别如图,线段PA的长叫切线长.·opAB如图,PA、PB是⊙O的切线,A、B为切点。连结OA、OB、OP,说明图中的PA与PB,∠APO与∠BPO有什么关系?为什么? PA、PB是⊙O的切线,A、B为切点∴OAPA⊥,OBPB⊥又 OA=OB,OP=OP∴RtAOPRtBOP△≌△∴PA=PB,∠APO=∠BPO切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。从前面切线的作图还有别的方法吗?切线长定理的基本图形的研究1.如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。(2)图中所有的垂直关系(3)图中所有的全等三角形(1)图中所有的等腰三角形(4)图中所有的相等关系(相等的角,相等的线段,相等的弧)((12除了PA=PB,∠1=2∠外,你还能得到哪些结论?(5)点D是△ABP的三条角平分线的交点吗?DEOPABCDCE2.如图:PA,PB分别切⊙O于点A和B,在AB上任取一点C,过点C作⊙O的切线,分别交PA、PB于点D、E。试探究:⑵∠DOE与∠AOB的关系.⑴△PDE的周长与PA,PB的关系;PA+PB∠AOB2OPAB((3)∠DOE与∠P的关系.12900-∠P总结切线的性质总结切线的性质1.切线和圆只有一个公共点;2.切线和圆心的距离等于圆的半径;3.圆的切线垂直于过切点的半径;4.如果圆的两条切线互相平行,则连结两个切点的线段是圆的直径;5.从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.。PBAO(3)连结圆心和圆外一点(2)连结两切点(1)分别连结圆心和切点反思:在解决有关圆的切线长问题时,往往需要我们构建基本图形。想一想想一想例1、已知:如图,P为⊙O外一点,PA,PB为⊙O的切线,A和B是切点,BC是直径.求证:ACOP∥.DCOPBA例2.如图:从⊙O外的定点P作⊙O的两条切线,分别切⊙O于点A和B,在弧AB上任取一点E,过点E作⊙O的切线,分别交PA、PB于点D、C.已知PA=7cm,(1)求△PCD的周长.(2)如果∠P=46°,求∠COD的度数C·OPBDAE思考:当E的位置变化时,(1)(2)中的结果变化吗?知识应用知识应用练习1.如图,已知PA,PB是⊙O的两条切线,A,B为切点,直线OP交⊙O于D,E交A,B于C(1)已知∠APB=660,求∠AEB与∠ADB的度数;(2)已知PA=4cm,PD=2cm,求半径OA的长及AB的长.((12DEOPABC练习2.如图,已知PA,PB,DE分别切⊙O于A,B,C三点,若PO=13cm,△PDE的周长为24cm,∠APB=400,(1)⊙O的半径,(2)∠EOD的度数.DCEOPAB小结1.经过圆外一点作圆的切线,这点和切点之间的线段的长叫做切线长2.从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。------切线长定理((12DEOPABC3.利用切线长的基本图形可以得到其他结论.作业1.如图,AB,CD与半圆O切于点A,D,且AB//CD,BC切⊙O于点E,若AB=4,CD=9,求⊙O的半径.ABDCO.EF2.如图,已知O是正方形ABCD一边BC的中点,AP与以O为圆心,OB为半径的半圆切于点T,求:AT:TP的值..PABDC.OT解:设AT=x,则AB=AD=DC=x,设PT=y,则PC=y,∴PD=x-y在Rt△ADP中1:4:404)()(2222222TPATyxxxyxyxyxxAPDPAD·ABCDEO21例2.如图,已知:在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆交AB于点E,AC切⊙O于点D。求证:DEOC∥证明:连接BD. ∠ABC=90°,OB为⊙O的半径∴CB是⊙O的切线 AC切⊙O于点D∴CD=CB,∠1=∠2∴OC⊥BD BE是⊙O的直径∴∠BDE...