证明题解题思路VIP免费

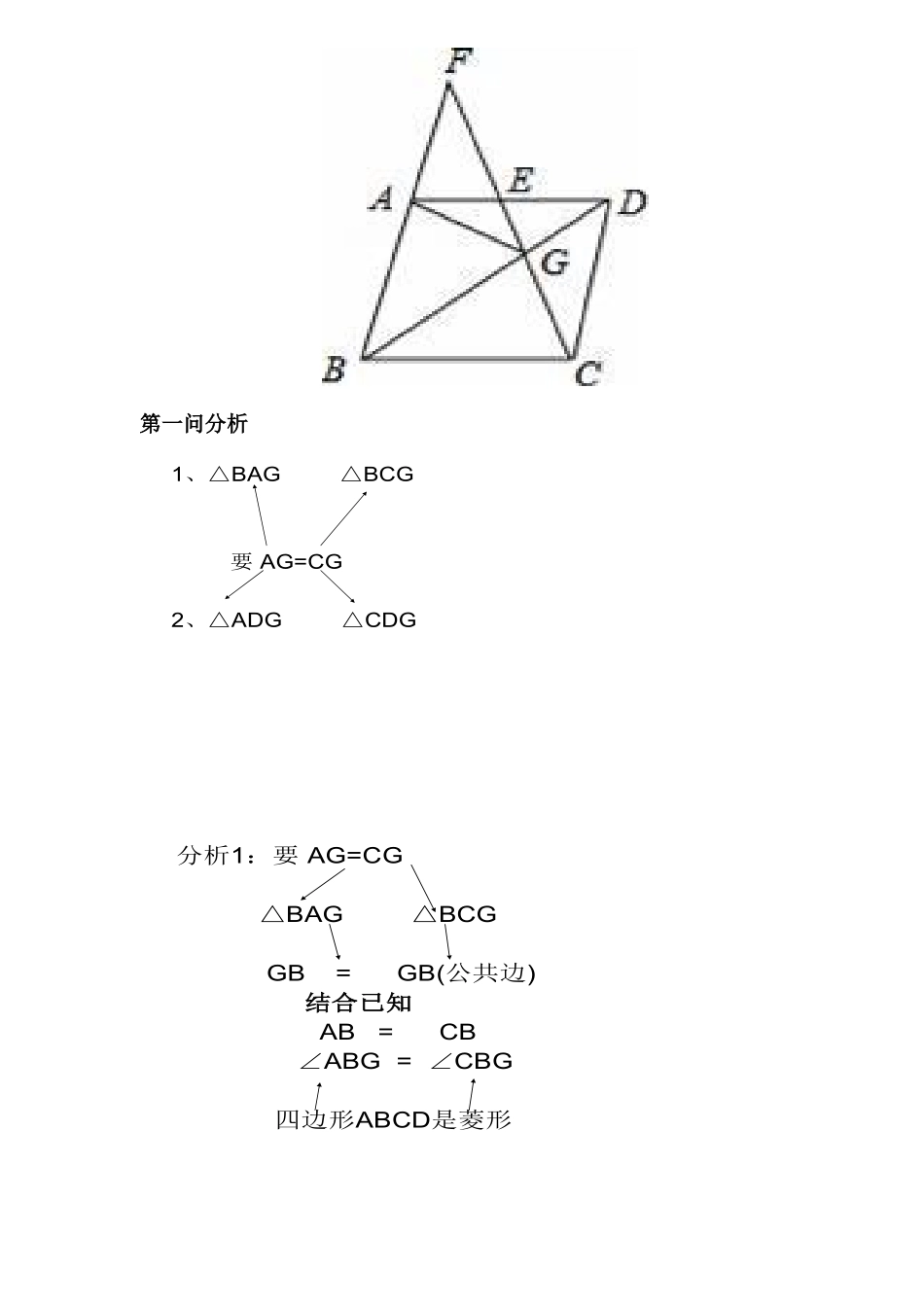
教学设计证明题的解题思路（一）证明题的解题思路：分析时从求证出发，结合已知，证题时把分析过程逆向写出就得。例1、已知：如图，D点△ABC在的AC边上，点E在AB边的延长线上，且AB·AE=AD·AC，求证：△ABC∽△ADE分析：（1）要证△ABC∽△ADE（从求证出发）（2）已有∠BAC=∠DAE(公共角)（结合已知）找另一对角相等夹这对角的对应边成比例（3）（难找出来）即→AB·AE=AD·AC（已知）AEACADABFABCED练习：(先写分析过程，再写证明过程)1、如图，矩形ABCD中，点F在CD上，且不与C,D重合，过点A作AF的垂线与CB的延长线相交于点E，求证：△ADF∽△ABEABCDEF2、如图，△ABC中，CE⊥AB于点E，BF⊥AC于点F，求证：△AEF∽△ACB。分析找角？∠A=∠A要证：△AEF∽△ACBAE/AC=AF/ABAE/AF=AC/AB△ACE∽△ABF．∠A=∠A结合已知∠AEC=∠AFBCE⊥AB于点E，BF⊥AC于点FABCEF证明：∵CE⊥AB，BF⊥AC，∴∠AEC=∠AFB=90°．∵∠A=∠A∴△ABF∽△ACE．∴AE/AF=AC/AB．∵∠A=∠A∴△AEF∽△ACB例2如图，在菱形ABCD中，G是BD上一点，连接CG并延长交BA的延长线于点F，交AD于点E。（1）求证：AG=CG．（2）求证：AG2=GE•GF第一问分析1、△BAG△BCG要AG=CG2、△ADG△CDG分析1：要AG=CG△BAG△BCGGB=GB(公共边)结合已知AB=CB∠ABG=∠CBG四边形ABCD是菱形分析2：要AG=CG△ADG△CDGGD=DG(公共边)结合已知AD=CD∠ADB=∠CDB四边形ABCD是菱形证明：（1）∵四边形ABCD是菱形，∴AB∥CD，AD=CD，∠ADB=∠CDB，在△ADG与△CDG中∴△ADG≌△CDG，∴AG=CG；方法3连接AC，根据菱形对角线互相垂直平分，G在AC的中垂线上，从而AG=CG；第二问(2)分析：AG2=GE•GF△AEG∽△FGA∠AGE=∠AGE(公共角)∠EAG=∠F结合已知△ADG≌△CDG∠DCG=∠EAGAB∥CD∠DCG=∠F证明：(2)∵△ADG≌△CDG∠DCG=∠EAGAB∥CD∠DCG=∠F∴∠EAG=∠F，∵∠AGE=∠AGE，∴△AEG∽△FGA，∴∴AG2=GE•GF．小结：证明题的解题思路：1、分析时从求证出发，结合已知，证题时把分析过程逆向写出就得。2、通过分析，往往会出现一题多解的情况，择优选取。3、有两问的题目，注意利用第一问为第二问服务。练习(2016·桂林模拟)如图，E，F分别是矩形ABCD的边AD，AB上的点，若EF＝EC且EF⊥EC.(1)求证：AE＝DC；(2)已知DC＝10，求BE的长．