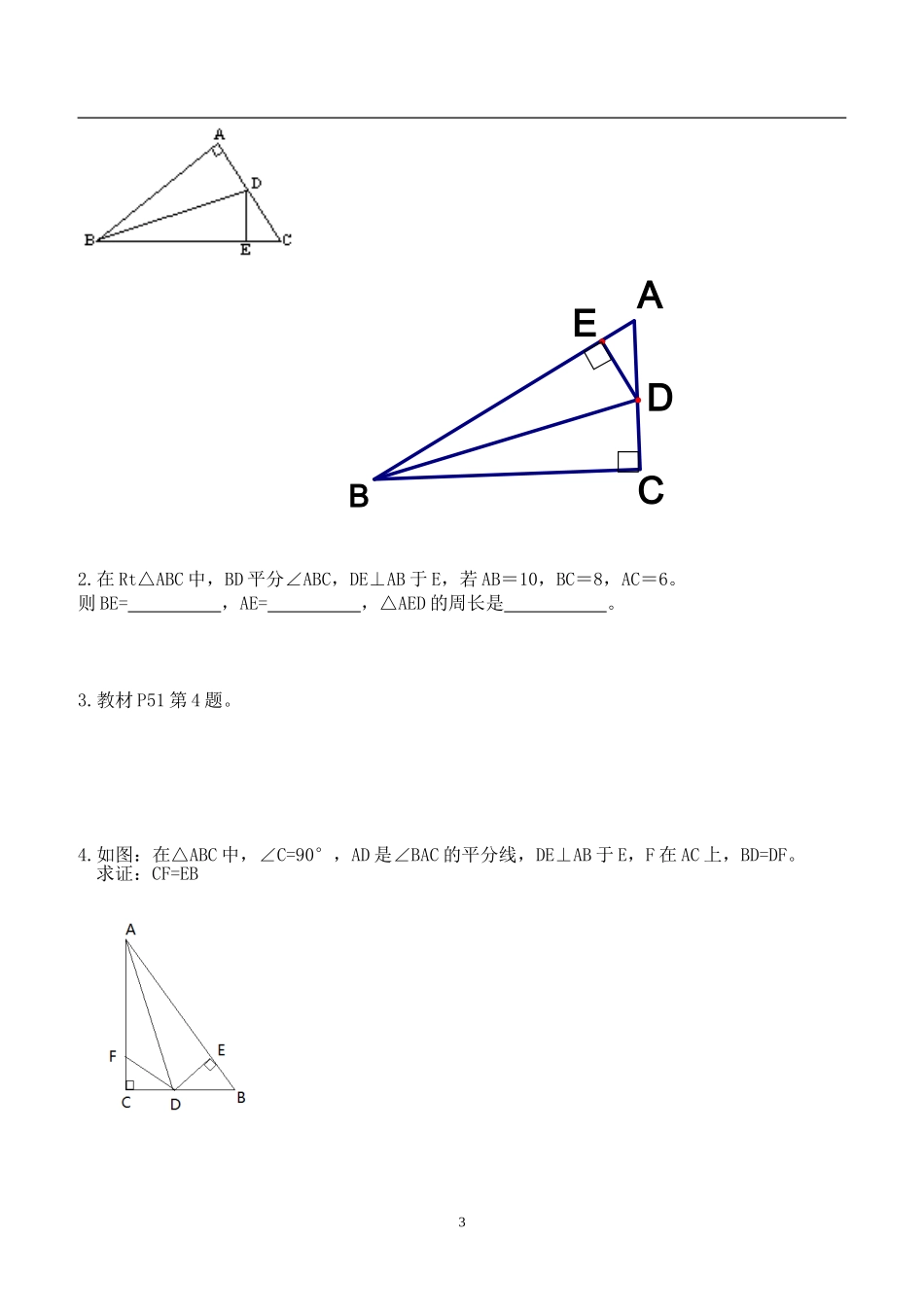
11.3角的平分线的性质(1)导学案班级_______姓名_____学习目标:1、掌握尺规作图作角平分线;2、通过探究理解角平分线的性质并会运用。学习重点:角平分线的性质【学习过程】●活动1用尺规作一个角的平分线1、已知:∠AOB求作:∠AOB的平分线OC作法:(1)以为圆心,适当长为半径作弧,交OA于M,交OB于N。(2)分别以M、N为圆心,的长为半径作弧,两弧在∠AOB内部交于点C。(3)画出射线OC,射线OC即为所求。●活动2实验、猜想角的平分线的性质(借助上图)操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA,PE⊥OB,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:观察测量结果,猜想线段PD与PE的大小关系,写出结论PDPE第一次第二次第三次●活动3用三角形全等证明性质已知:如图,OC平分∠AOB,点P在OC上,PD⊥OA于D,PE⊥OB于E1求证:PD=PE证明:●活动4归纳角平分线的性质:符号语言:∵OC是∠AOB的平分线,∴一般情况下,我们要证明一个几何中的命题时,会按照类似的步骤进行,即:(1);(2);(3)。应用:例如图,ΔABC的角平分线BM,CN相交于点P。求证:点P到三边AB,BC,CA的距离相等。练习:1.如图所示,在△ABC中,∠A=90°,BD平分∠ABC,AD=2cm,则点D到BC的距离为________cm.22.在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,若AB=10,BC=8,AC=6。则BE=,AE=,△AED的周长是。3.教材P51第4题。EDCBA4.如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF。求证:CF=EB3