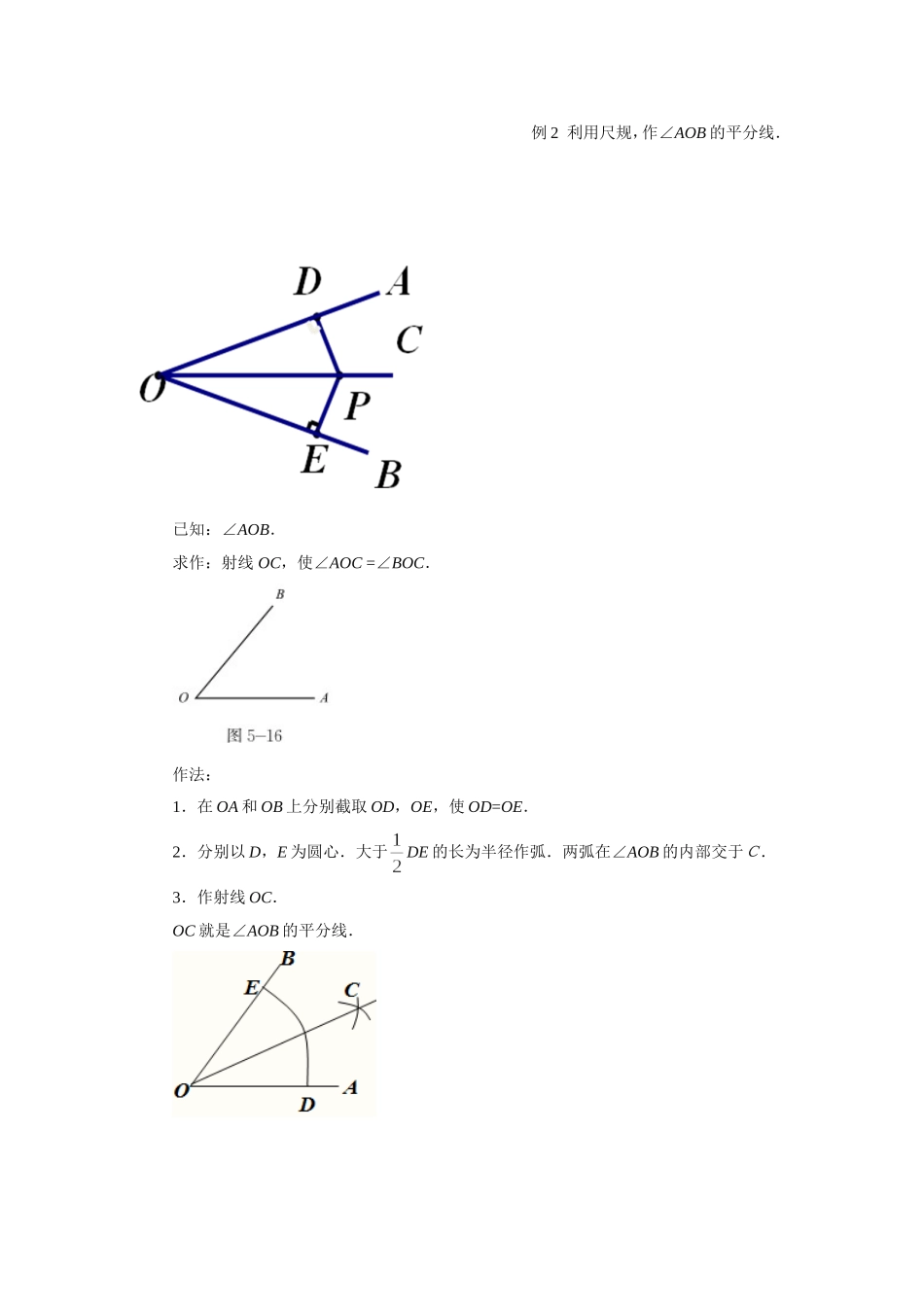
《简单的轴对称图形》教案教学目标一、知识与技能1.使学生掌握等腰三角形和等边三角形的轴对称性及其有关性质;2.掌握作已知角的平分线的尺规作图方法;二、过程与方法1.经历探索的过程,养成善于观察的习惯,从不同的情境中,通过思考、分析,总结共性,学会学习;2.在探究作已知角的平分线的方法和角平分线的性质的过程中,发展几何直觉;三、情感态度和价值观1.培养学生的抽象思维和空间观念,结合教学进行审美教育,让学生充分感知数学美,激发学生热爱数学的情感;2.使学生在自主探索角平分线的过程中,经历画图、观察、比较、推理、交流等环节,从而获得正确的学习方式和良好的情感体验;教学重点对性质的理解及探索过程教学难点应用性质解决一些实际问题教学方法引导发现法、启发猜想课前准备教师准备课件、多媒体;学生准备三角板,练习本;课时安排1课时一.复习引入1、从一个角的顶点出发,把这个角分成两个角的射线叫做这个角的角平分线。2、什么是点到直线的距离?二.新课角是轴对称图形吗?如图5-16,将∠AOB对折,你发现了什么?体验角平分线的简易作法,并为角平分线的性质定理的引出做铺垫,为下一步设置问题墙。结论:角是轴对称图形,角平分线所在的直线是它的对称轴.做一做(1)在一张纸上任意画∠AOB,沿角的两边将角剪下,将这个角对折,使角的两边重合;(2)在折痕(即角平分线)上任意取一点C,过点C分别向∠AOB的两边折垂线,垂足分别为D,E,将∠AOB再次对折,折痕CD与CE能重合吗?改变点C的位置,CD和CE还相等吗?角平分线的性质角平分线上的点到这个角的两边的距离相等.验证角平分线定理已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E。求证:PD=PE证明:∵PD⊥OA,PE⊥OB(已知)∴∠PDO=∠PEO=90(垂直的定义)∵OC是∠AOB的平分线∴∠POD=∠POE在△PDO和△PEO中∠PDO=∠PEO∠AOC=∠BOCOP=OP∴△PDO≌△PEO∴PD=PE使用方法几何语言:∵OC是∠AOB的平分线,又PD⊥OA,PE⊥OB∴PD=PE例2利用尺规,作∠AOB的平分线.已知:∠AOB.求作:射线OC,使∠AOC=∠BOC.作法:1.在OA和OB上分别截取OD,OE,使OD=OE.2.分别以D,E为圆心.大于DE的长为半径作弧.两弧在∠AOB的内部交于C.3.作射线OC.OC就是∠AOB的平分线.明确几何作图的基本思路和方法.培养学生运用直尺和圆规作已知角的平分线的能力.让学生体验成功。三、习题1,作任意两角的平分线,交点是P点画一个三角形,作任意两角的平分线,交点为P,过P点分别作垂线你有什么发现?再作第三角的平分线,是否过这一点四、拓展某一天,我校七年级的同学参加义务劳动,其中七(1)班的同学分别在M、N两处参加劳动,七(2)班的同学分别在道路AB、AC两处劳动,现要在道路AB、AC的交叉区域内设一个荼水供应点P,使P到两条道路的距离相等,且使PM=PN,请你找出点P的位置,并说明理由。五、小结通过本节课的内容,你有哪些收获?MNPB