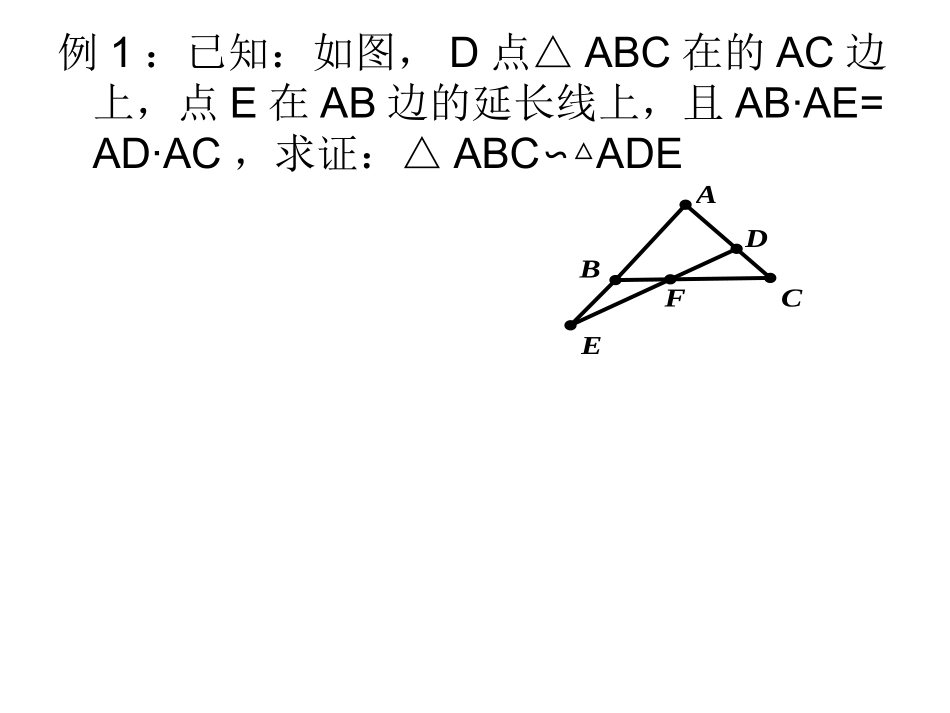
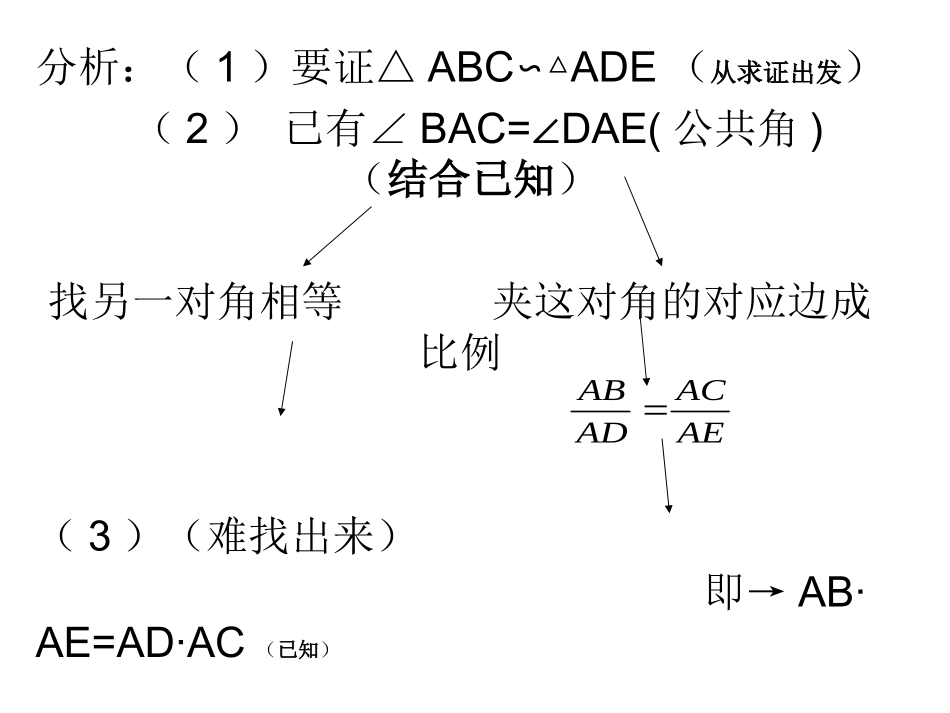
证明题的解题思路南渡镇第一中学陈宇例1:已知:如图,D点△ABC在的AC边上,点E在AB边的延长线上,且AB·AE=AD·AC,求证:△ABCADE∽△FABCED分析:(1)要证△ABCADE∽△(从求证出发)(2)已有∠BAC=DAE(∠公共角)(结合已知)找另一对角相等夹这对角的对应边成比例(3)(难找出来)即→AB·AE=AD·AC(已知)AEACADAB小结1、证明题的解题思路:分析时从求证出发,结合已知,证题时把分析过程逆向写出就得。•练习:(先写分析过程,再写证明过程)•1、如图1矩形ABCD中,点F在CD上,且不与C,D重合,过点A作AF的垂线与CB的延长线相交于点E,求证:△ADF∽ABE△ABCDEF•2、如图2,△ABC中,CEAB⊥于点E,BFAC⊥于点F,求证:△AEFACB∽△。ABCEF分析找角?∠A=A∠要证:△AEFACB∽△AE/AC=AF/ABAE/AF=AC/AB△ACEABF∽△.∠A=A∠结合已知∠AEC=AFB∠CEAB⊥于点E,BFAC⊥于点FABCEF证明:∵CEAB⊥,BFAC⊥,∴∠AEC=AFB=90°∠.∵∠A=A∠∴△ABFACE∽△.∴AE/AF=AC/AB.∵∠A=A∠∴△AEFACB∽△ABCEF例2如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E。•(1)求证:AG=CG.•(2)求证:AG2=GE•GF.1、△BAGBCG△要AG=CG2、△ADGCDG△分析1:要AG=CG△BAGBCG△GB=GB(公共边)结合已知AB=CB∠ABG=CBG∠四边形ABCD是菱形分析2:要AG=CG△ADGCDG△GD=DG(公共边)结合已知AD=CD∠ADB=CDB∠四边形ABCD是菱形(1)∵四边形ABCD是菱形,∴ABCD∥,AD=CD,∠ADB=CDB∠,在△ADG与△CDG中∴△ADGCDG≌△,∴AG=CG;(1)分析3:连接AC,根据菱形对角线互相垂直平分,G在AC的中垂线上,从而AG=CG;(2)分析:AG2=GE•GF△AEGFGA∽△∠AGE=AGE∠(公共角)∠EAG=F∠结合已知△ADGCDGDCG=EAG≌△∠∠ABCD∥DCG=F∠∠(2)ADGCDG∵△≌△∠DCG=EAG∠ABCD∥∠DCG=F∠∴∠EAG=F∠,∵∠AGE=AGE∠,∴△AEGFGA∽△,∴∴AG2=GE•GF.小结:2、通过分析,往往会出现一题多解的情况,择优选取。3、有两问的题目,注意利用第一问为第二问服务练习3、(南宁)如图,ABFC∥,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.(1)求证:△ADECFE≌△;(2)若GB=2,BC=4,BD=1,求AB长.(1)证明:∵ABFC∥,∴∠A=∠FCE.又∠AED=∠FEC.DE=EF∴△ADECFE(≌△AAS).(2)ABFC∵∥,∴△GBDGCF.∽△∴GBGC∶=BDCF.∶∵GB=2,BC=4,BD=1,∴26∶=1CF.CF∶∴=3.∵△ADECFE≌△,∴AD=CF.∴AB=AD+BD=4.4、(2016·桂林模拟)如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC且EFEC.⊥•(1)求证:AE=DC;•(2)已知DC=10,求BE的长.(1)证明:∵EFEC⊥,∴∠CEF=90°,∠3+∠2=90°.又∵∠1+∠2=90°,∴∠1=∠3.在矩形ABCD中有∠A=∠D.又EF=CE∴△AEFDCE.≌△∴AE=DC.(2)由(1)可知AE=DC=10,AB=DC=10,BE=?小结:证明题的解题思路:1、分析时从求证出发,结合已知,证题时把分析过程逆向写出就得。2、通过分析,往往会出现一题多解的情况,择优选取。3、有两问的题目,注意利用第一问为第二问服务。