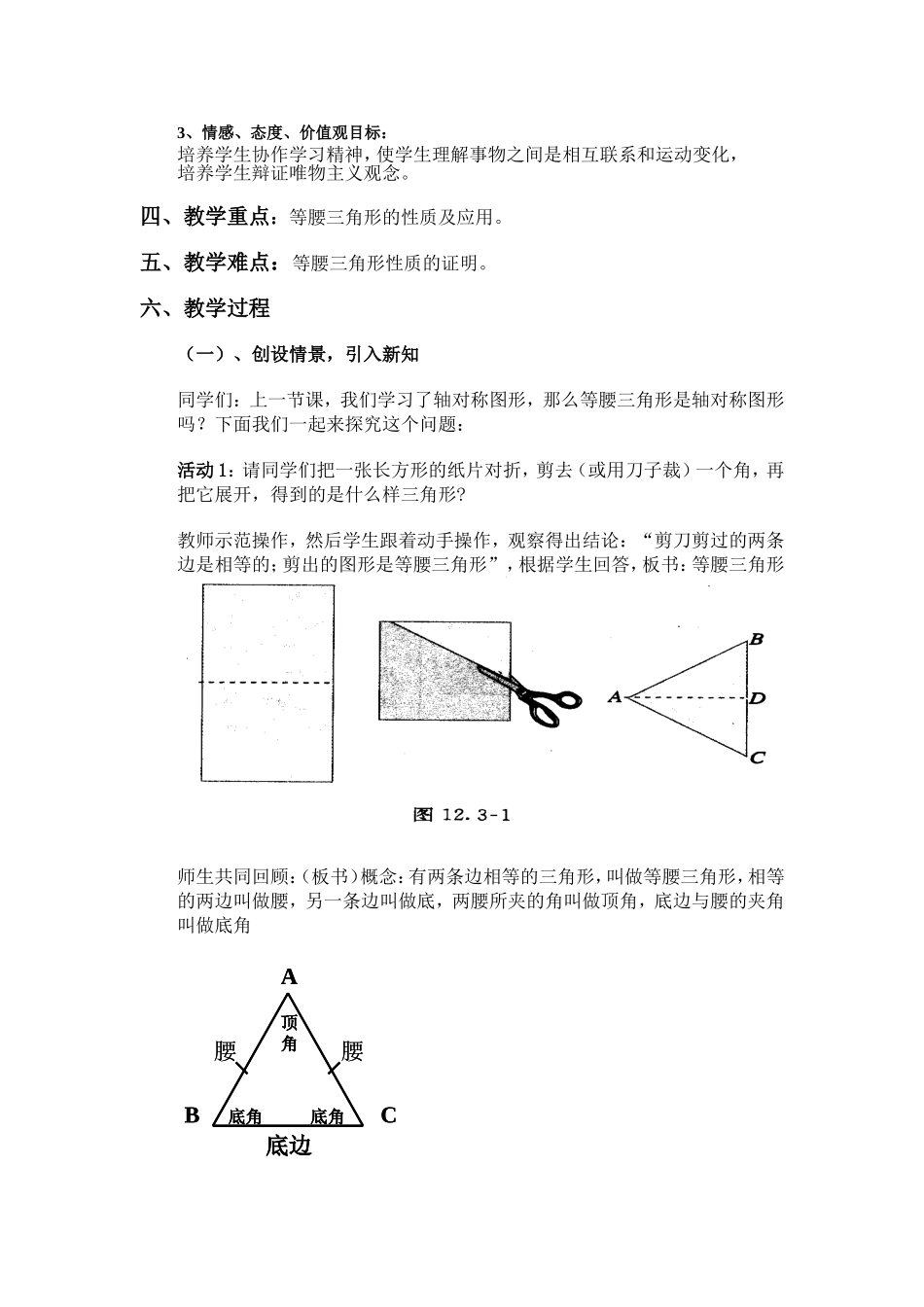
八年级数学《等腰三角形(一)》教学设计南宫市段芦头中学陈瑞雪一、教材及教学内容分析㈠教材的地位和作用分析等腰三角形是新人教版八年级上册十三章第三节等腰三角形的第一课时的内容。本节课是在前面学习了三角形的有关概念及性质、轴对称变换、全等三角形、垂直平分线和尺规作图的基础上,研究等腰三角形的定义及其重要性质,它既是前面所学知识的延伸,也是后面直角三角形、等边三角形的知识的重要储备,我们常常利用它证明角相等、线段相等、两直线垂直,因此本节课具有承上启下的重要作用。㈡教学内容的分析本节课是等腰三角形的第一堂课,在认识等腰三角形的基础上着重介绍“等腰三角形的性质”。让学生通过动手剪等腰三角形、对折等腰三角形等活动,探究发现等腰三角形的性质,经历知识的“再发现”过程。在探究活动的过程中发展创新思维能力,改变学生的学习方式。在发现等腰三角形的性质的基础上,再经过推理证明等腰三角形的性质,使得推理证明成为学生观察、实验、探究得出结论的自然延伸,有机地将等腰三角形的认识与等腰三角形的性质的证明结合起来,从中发展学生推理能力。二、设计思想本课内容在初中数学教学中起着比较重要的作用,它是对三角形的性质的呈现。教材通过学生对等腰三角形的叠合操作,得出等腰三角形的轴对称性,给出了等腰三角形的性质1,并对性质1进行了证明,从性质1的证明过程中,得出等边三角形性质及等腰三角形性质2,这里“等边对等角是今后证明两角相等常用方法之一,而等腰三角形的“三线合一”是今后证明两条线段相等、两个角相等及两条直线互相垂直的重要依据。运用观察、操作来领悟规律,以全等三角形为推理工具,在交流中突破难点。采用直观教学发现法和启发诱导教学法,与学生实践操作、合作探究。三、教学目标1、知识与能力目标:①掌握等腰三角形的性质及其两个推论。②运用等腰三角形的性质及其推论进行有关证明和计算。2、过程与方法目标:①让学生体验等腰三角形是一个轴对称性图形。②经历操作、发现、猜想、证明的过程,培养学生的逻辑思维能力。3、情感、态度、价值观目标:培养学生协作学习精神,使学生理解事物之间是相互联系和运动变化,培养学生辩证唯物主义观念。四、教学重点:等腰三角形的性质及应用。五、教学难点:等腰三角形性质的证明。六、教学过程(一)、创设情景,引入新知同学们:上一节课,我们学习了轴对称图形,那么等腰三角形是轴对称图形吗?下面我们一起来探究这个问题:活动1:请同学们把一张长方形的纸片对折,剪去(或用刀子裁)一个角,再把它展开,得到的是什么样三角形?教师示范操作,然后学生跟着动手操作,观察得出结论:“剪刀剪过的两条边是相等的;剪出的图形是等腰三角形”,根据学生回答,板书:等腰三角形师生共同回顾:(板书)概念:有两条边相等的三角形,叫做等腰三角形,相等的两边叫做腰,另一条边叫做底,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角A顶角腰腰B底角底角C底边A顶角腰腰B底角底角C底边教师提问:剪出的三角形是轴对称图形吗?你能发现这个三角形有哪些特点吗?说一说你的猜想学生思考并发表自已的看法,教师提出本节课所要解决的问题师生归纳:等腰三角形是轴对称图形,底边上的中线所在的直线是它的对称轴(板书)教师说明:对称轴是一条直线,而三角形的中线是线段,因此不能说等腰三角形底边上的中线是它的对称轴。(二)、合作交流,探索新知活动2:教师出示刚才剪下的等腰三角形纸片,标上字母如图所示:把边AB叠合到边AC上,这时点B与C重合,并出现折痕AD,观察图形,△ADB与△ADC有什么关系?图中哪些线段或角相等?AD与BC垂直吗?为什么?学生回答:△ADB与△ADC重合,则角∠B=∠C∠BAD=∠CAD,∠ADB=∠CDA从而,AD⊥BC线段AB=ACBD=CDAD=AD活动3:由上面的性质我们可以得到等腰三角形如下性质:性质1:等腰三角形的两个底角相等,简称:等边对等角(板书)性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合简称“三线合一”教师提问:这两个命题的题设是什么?结论是什么?学生可结合图形回答(板书)已知:在△ABC中,AB=AC求证:∠B=...