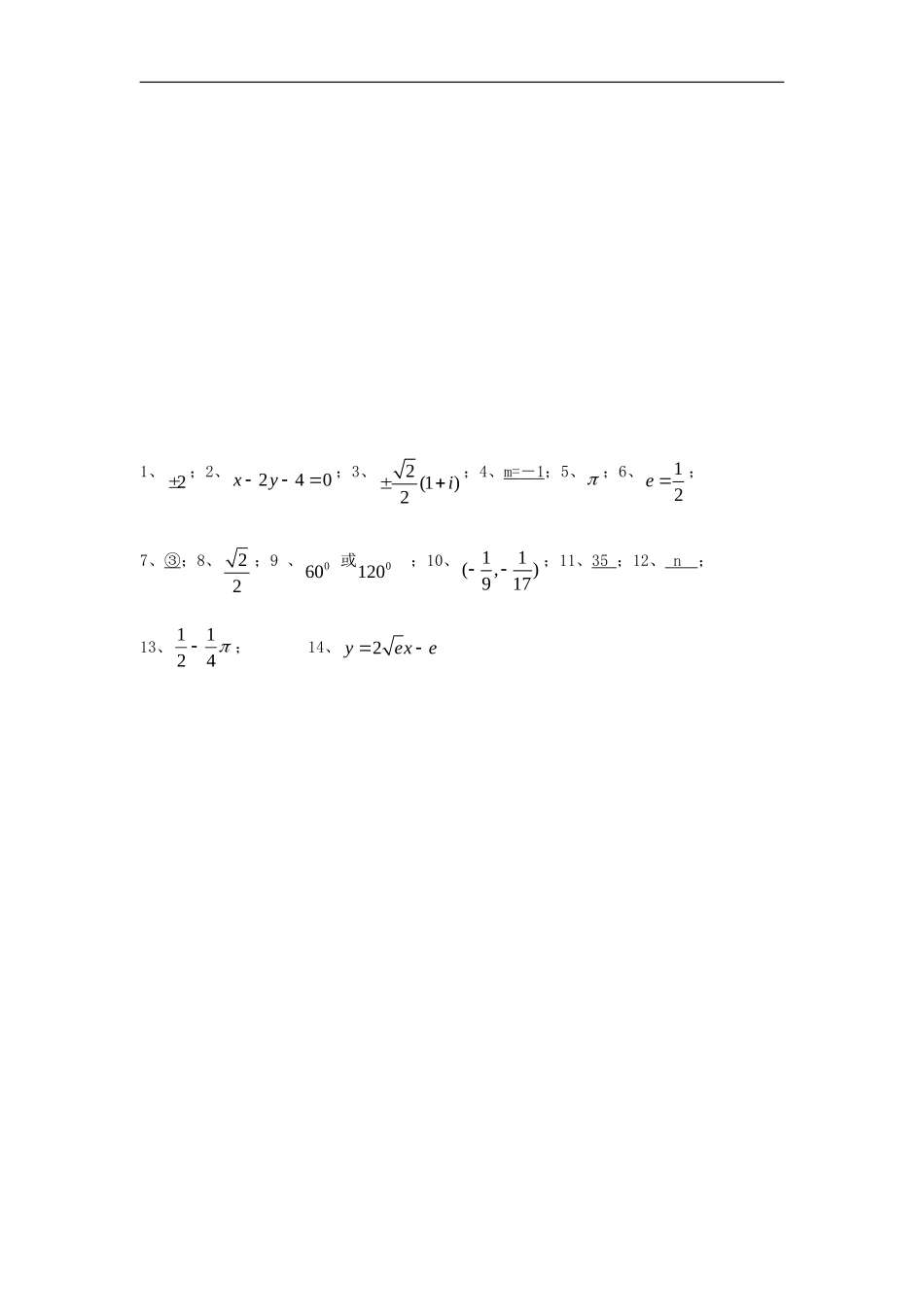江苏省2012届高三数学二轮专题训练:填空题(84)本大题共14小题,请把答案直接填写在答题位置上。1.已知集合},1{},2,0{2aBA,若}4,2,1,0{BA,则实数a=▲2.经过点)1,2(,与向量(1,2)AB�垂直的直线方程是▲3.已知复数z满足:2,()zii是虚数单位,则z=▲4.已知向量(0,1),(1,3),(,),OAOBOCmm�若A、B、C三点共线,则实数m=▲5.函数()sin(sincos)fxxxx的周期T=▲6.已知点(,)(0)Pabab与椭圆22221xyab的两个焦点12,FF构成等腰三角形,则椭圆的离心率e=▲7.设,为两个不重合的平面,,,mnl是不重合的直线,给出下列命题,其中正确的序号是▲①若,,mnm则n∥;②若,,nm,相交不垂直,则n与m不垂直;③若,,,mnmn,则n;④m是平面的斜线,n是m在平面内的射影,若nl,则ml.8.设点P是曲线2lnyxx上的任意一点,则点P到直线1yx的最小距离为▲9.在ABC中,2223tanbcaacB,则角B=▲10.通项公式为2naann的数列na,若满足12345aaaaa,且1nnaa对8n恒成立,则实数a的取值范围是▲11.把形如(,)nMmmnN的正整数表示为各项都是整数、公差为2的等差数列的前m项和,称作“对M的m项划分”。例如:293135,称作“对9的3项划分”;把64表示成364413151719,称作“对64的4项划分”.据此,对324的18项划分中最大的数是▲12.设11()(),()[()](2,)1nnxfxfxfxffxnnNx,则12(1)(2)()(1)(1)(1)nfffnfff=▲13.在ABCRt中,90C,,2BCACD是ABC内切圆圆心,设P是⊙D外的三角形ABC区域内的动点,若CBCACP,则点),(所在区域的面积为▲14.若存在实常数k和b,使函数()fx和()gx对其定义域上的任意实数x恒有:()fxkxb和()gxkxb,则称直线:lykxb为()fx和()gx的“隔离直线”。已知2(),()2lnhxxxex,则可推知(),()hxx的“隔离直线”方程为▲1、2;2、240xy;3、2(1)2i;4、m=-1;5、;6、12e;7、③;8、22;9、060或0120;10、11(,)917;11、35;12、n;13、4121;14、2yexe