1011高数A(一)试题及解答VIP免费

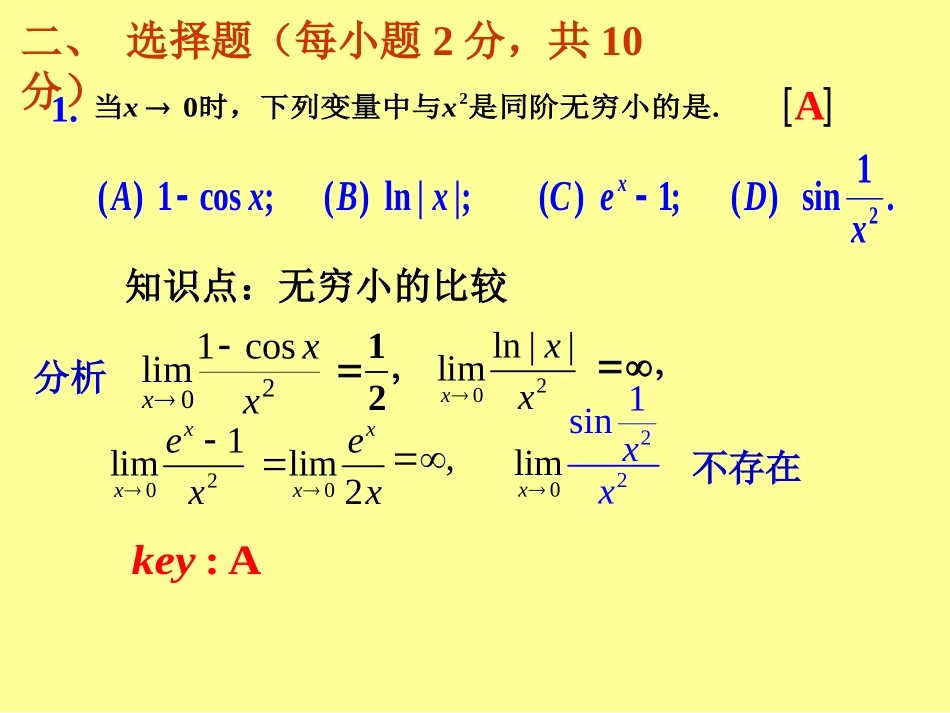
济南大学2010~2011学年第一学期（A）课程考试试卷评分标准（含参考答案）一、填空题（每小题3分，共15分）10233sin21.lim(1),02.(),03.4.(1)(1)xxxxxxxfxaaxyxexxdx设在原点连续，则的微分是21e11336246241133xxxxC2323()xxxedx205.xedx121.2.0xx当时，下列变量中与是同阶无穷小的是二、选择题（每小题2分，共10分）知识点：无穷小的比较:Akey21()1cos;()ln||;()1;()sin.xAxBxCeDxA分析20cos1limxxx12，20ln||limxxx，201limxxex0221silinmxxx0lim2xxex,不存在2.21()0xfxexfx设,则是的.分析知识点：函数间断点的类型，();();();().ABCD可去间断点跳跃间断点无穷间断点振荡间断点:Akey第一类间断点可去间断点跳跃间断点左右极限都存在第二类间断点无穷间断点振荡间断点左右极限至少有一个不存在在点间断的类型A22121000limlimlimxxxxxxeeeee000000000()()()()()()()()()()()()AfxxxfxxxBfxxxfxxxCfxxxfxxxDfxxxfxxx下列结论正确的是[]若在点连续，则在点可导；若在点可导，则在点连续；若在点连续，则在点可微；若在点可微，则在点也可能可导.3.:BkeyB分析极限存在连续可导可微00()(,)()(),()....fxabfxfxfxABCD若函数在开区间内，则函数在此区间内是（）单调减少，曲线凸的单调增加，曲线凸的单调减少，曲线凹的单调增加，曲线凹的:Ckey利用函数的一阶导数和二阶导数符号判断函数的单调性和凹凸性.分析C4.5.下列等式正确的是.知识点：不定积分和导数的关系，d();();d()().;baAdfxfxBfxdxfxCxCdfxdxfxdxDfxdxfxC:Dkey微分运算与求不定积分的运算是互逆互逆的.)()(xfdxxfdxddxxfdxxfd)(])([CxFdxxF)()(CxFxdF)()(分析D三、求极限（每小题8分，共16分）20sin1limxxexx1.解：0coslim2xxexx原式0sinlim2xxex1.22sin030sinlimxtxedtxx2.解：2sin20coscoslim3xxexxx原式2sin201lim3xxex2sin02sincoslim6xxexxx1.32sin20cos(1)lim3xxxex2sin030sinlimxtxedtxx2.另解：2sin20coscoslim3xxexxx原式2sin201lim3xxex220sinlim3xxx1.32sin20cos(1)lim3xxxex四、计算题（每小题8分，共16分）11arctan,.xyyx设求1.解：221111111()xxyxxx211.x四、计算题（每小题8分，共16分）tan(),.yxyy设求2.解：21sec()()yxyy221csc()cot()().yxyxyy方程两边对x求导,得2csc()yxy所以222csc()cot()(1csc())xyxyxy232csc()cot()xyxy五、计算题（每小题8分，共16分）1.231.(1)dxx知识点：不定积分的计算方法，第二换元积分法，解tan,,22xtt设22sec,dxtdt原式231secdsectttcosdttsintC21xCx………9分……3分………6分五、计算下列积分（每小题8分，共16分）220cos.xxdx2.2sin2sinxxxxdx2sin2(coscos)xxxxxdxC解则令2,uxcos(sin)dvxdxdx22,dudxxdxsinvx原式22220022cos[sincossin]xxdxxxxxx4.2sin2cos2sinxxxxxC五、计算下列积分（每小题8分，共16分）220cos.xxdx2.2200[2cos]2cosxxxdx4解222002[sin]sinxxxxdx原式六、综合题（每小题10分，共20分）2(0,0)1ypxqxpqxy抛物线与直线相切，1.解由抛物线与直线相切,有唯一解，故3322408(),63(1)qpqqSpxqxdxpq2120,,qypxqxxxxp与轴交点的横坐标为21ypxqxxypqx问当,为何值时，抛物线与轴所围图形的面积最大.21(1).4pq1xy2ypxqx所围图形面积为可知方程组六、综合题（每小题10分，共20分）1.解3322408(),63(1)qpqqSpxqxdxpq258(3)0,3.3(1)qqSqq令得030;qS当时,30...