3、圆周运动的案例分析VIP免费

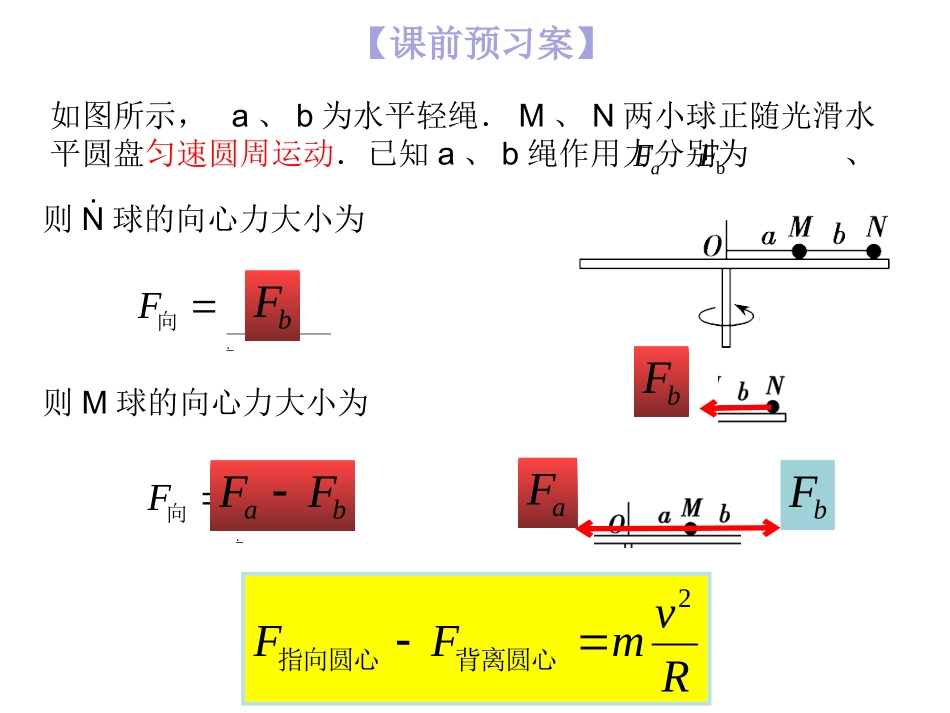
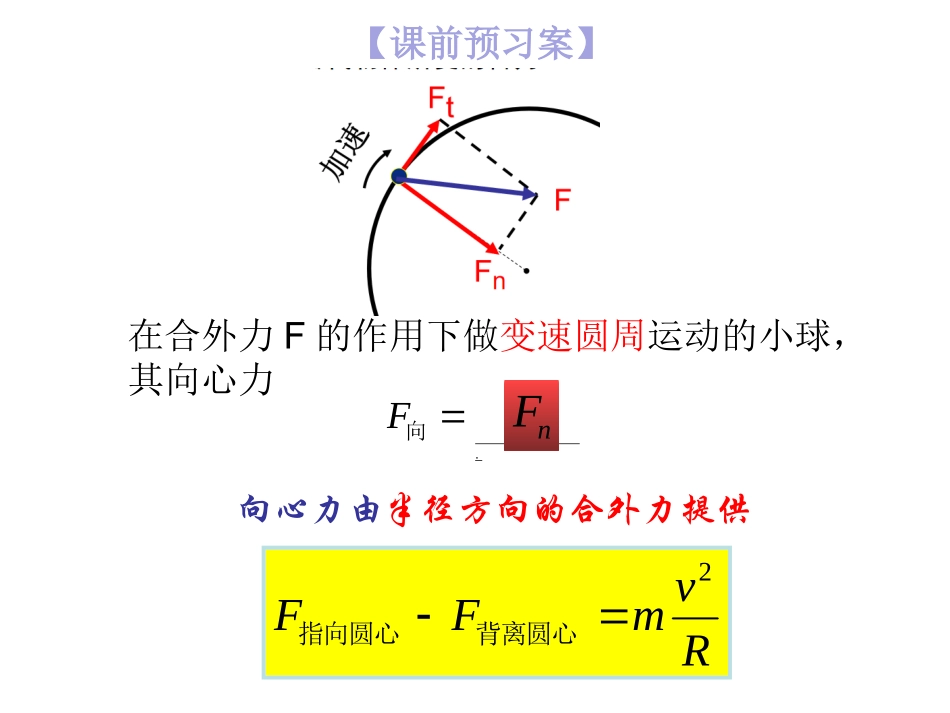
圆周运动的案例分析二竖直面内的圆周运动【课前预习案】如图所示，a、b为水平轻绳．M、N两小球正随光滑水平圆盘匀速圆周运动．已知a、b绳作用力分别为、.aF则N球的向心力大小为bF.向FbF则M球的向心力大小为.向FbaFFbFbFaFRvmFF2背离圆心指向圆心【课前预习案】在合外力F的作用下做变速圆周运动的小球，其向心力向F.nF向心力由半径方向的合外力提供RvmFF2背离圆心指向圆心生活中竖直面内圆周运动展示【课前预习案】生活中竖直面内圆周运动展示【课前预习案】“轻绳模型”生活中竖直面内圆周运动展示【课前预习案】“轻杆模型”生活中竖直面内圆周运动展示【课前预习案】“拱桥”模型三个模型【课堂探究案】“轻杆模型”“拱桥”模型“轻绳模型”Fmg（2）要让小球完成完整的圆周运动，绳子的拉力必须满足什么条件？最小速度多大？（1）在上图中作出小球在最高点时的受力分析绳子必须绷直：重力提供向心力：Rvmmg20Finm最小速度为：gRv（3）当最高点速度时小球恰好做完成圆周运动；要使小球能够通过最高点，小球在最高点的速度gRvgRv【课堂探究案】例1杂技演员表演“水流星”时，一根绳子系着盛水的两个杯子，演员抡起绳子中央，杯子就做圆周运动，而且水不从杯里洒出，甚至杯子在竖直面内运动到最高点时，已经杯口朝下，水也不会从杯里洒出来，如图所示．设水的质量为m＝0.5kg，绳子总长为2L＝1.6m，g取10m/s2.求：(1)在最高点水不流出的最小速率；(2)在最高点速率v＝4m/s时，水对杯底的压力．【课堂探究案】解：(1)设最小速率为v0，重力提供向心力mg＝mv02L解得v0＝22m/s(2)由于v大于v0，对水受力分析如图所示，由牛顿第二定律得F压＋mg＝mv2L，解得F压＝5N.由牛顿第三定律知，水对杯底的作用力F压′＝F压＝5N，方向竖直向上．mg压F小球最高点的最小速度：0inmvmgNF0-mgFNmgFN【课堂探究案】mg拉FmgNFmg假设当小球速度为时的受力情况如左图所示：0NFgRvgRv0当gRv当杆对球有支持力：杆对球有拉力：vRvmFmgN2-RvmmgFN2-mgNF当0NF0NF球仅受重力：例2.长L＝0.4m、质量可忽略的细杆，其一端可绕O点在竖直平面内转动，另一端固定着一个可看成质点的小球A.A的质量m＝2kg，如图所示，当A通过最高点时，g取10m/s2，求在下列两种情况下杆对小球的力：(1)A在最高点的速度为1m/s；(2)A在最高点的速度为4m/s.方法一当小球恰好通过最高点时，由牛顿第二定律有：Lvmmg2解得：smv/2（1）由于小球速度为V1=1m/s<2m/s,杆对小球作用力为支持力，方向向上。受力分析如下mgNFLvmFmgN21-解得：NFN15（2）由于小球速度为V2=4m/s>2m/s,杆对小球作用力为拉力，方向向下。受力分析如下mg拉FLvmFmg22拉解得：NF60拉方法二假设当小球速度为V时,小球的受力分析如下：LvmFmg2解得：NF15-（1）把小球速度V=1m/s代入mgF①①负号表示杆对小球的力方向向上，为支持力，大小为15N.解得：NF60（2）把小球速度V=4m/s代入①正值表示杆对小球的力方向向下，为拉力，大小为60N.(1)明确运动的类型，是细绳模型还是轻杆模型．(2)明确物体的临界状态，即在最高点时物体具有最小速度时的受力特点．(3)分析物体在最高点及最低点的受力情况，根据牛顿第二定律列式求解．(4)有时某个力不方便直接求解，可应用牛顿第三定律，转换研究对象，先求其反作用力，然后再求该力．竖直平面内圆周运动的分析方法小结【课堂探究案】RvmFF2背离圆心指向圆心1.（多选）如图所示，质量为m的小球在竖直平面内的光滑圆环内侧做圆周运动，圆环半径为R，小球经过圆环内侧最高点时刚好不脱离圆环，则其通过最高点时下列表述正确的是（）D.小球的向心加速度大小等于gA.小球对圆环的压力大小等于mgB.重力mg充当小球做圆周运动所需的向心力C.小球的线速度大小等于【课堂探究案】·O刚好不脱离最高点环对小球无压力，小球仅受重力,充当向心力.Rvmmg2向mamgBCD练习2．如图所示，可视为质点的、质量为m的小球，在半径为R的竖直放置的光滑圆形管道内做圆周运动，下列有关说法中正确的是()A.小球能够到达最高点时的最小速度为0B.小球能够通过最高点时的最小速度为C.如果小球在...