任意角的三角函数(1)VIP免费

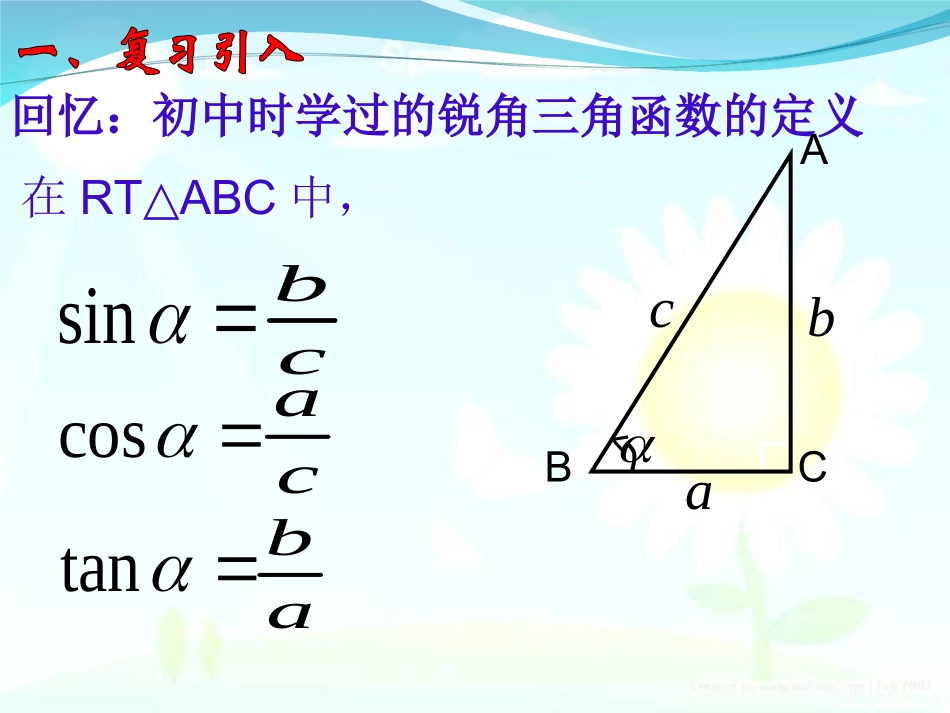
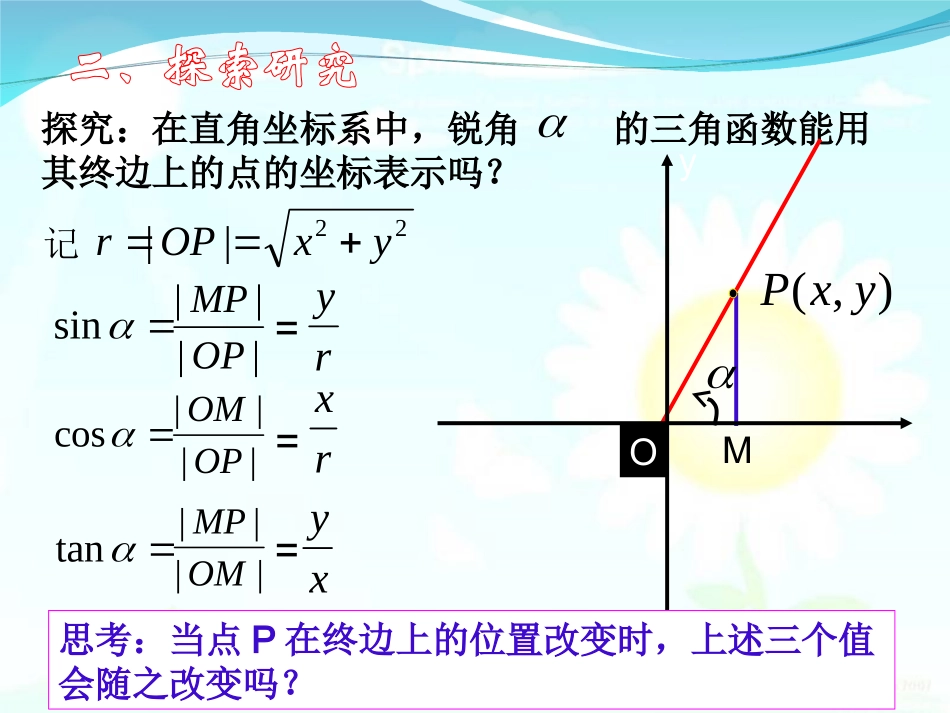
高一数学组回忆：初中时学过的锐角三角函数的定义在RTABC△中，sincostanbacACBcbcaab探究：在直角坐标系中，锐角的三角函数能用其终边上的点的坐标表示吗？OxyM),(yxP22||yxOPr记rysin||||OPMP=rxcos||||OPOM=tan||||OMMP=xy思考：当点P在终边上的位置改变时，上述三个值会随之改变吗？如果改变点Ｐ在终边上的位置，这三个比值会改变吗？﹒PMOPMPsinOPOMcosOMMPtanOMP∽PMOPOPMPOOMMOPM诱思探究MOyxP(a,b)由相似三角形的知识，对于确定的角α，这三个比值不会随P在α的终边上的位置的改变而改变。A(1,0)OxyM),(yxPyxxy思考：为了使sinα，cosα的表示式更简单，你认为点P的位置选在何处最好？此时，sinα，cosα分别等于什么？rysin=rxcosxytan==22||yxOPr)1(22yx在直角坐标系中，称以原点O为圆心，以单位长度为半径的圆为单位圆。如图，设α是一个任意角，它的终边与单位圆交于点P(x,y)，那么：（1）y叫做α的正弦（sine），记作sinα，即sinα＝y（2）x叫做α的余弦（cosine），记作cosα，即cosα＝xOxyP(x，y)A(1,0)（3）叫做α的正切（tangent），记作tanα，即tanα＝（x≠0）xyxy所以，正弦，余弦，正切都是以角为自变量，以单位圆上点的坐标或坐标的比值为函数值的函数，我们将他们称为三角函数.Oxy)21,23(M【练习】求角的三个三角函数值。67,2167sin,2367cos.2367tan67例2已知角的终边过点P（－3，－4），求角的正弦、余弦和正切值.可求出相应的三角函数值。A(1,0)OP(x,y)P0(-3,-4)M0xyαM分析：∽OMPPMO00如图，设角α的终边与单位圆交于点P（x,y).分别过点作x轴的垂线MP,M0P0,pp0,;541sin00OPOPMPyyPM;531cos00PMOOOPOMxx5)4()3(220pO解：由已知可得：于是，xA(1,0)yOP(x,y)αP0(-3,-4)M0M.34cossintanxy则0OMPPMO00∽,,3,,4000xOMOyMPMPMOαxy一般地，设角终边上任意一点的坐标为（x,y）它与原点的距离是r,则,sinry.tanxyP(x,y)M0r,cosrxOxy)5,12(PM【练习】,135sinry,1312cosrx.125tanxy135)12(22rop)5,12(P已知角的终边过点,求角的三个三角函数值。)5,12(P1、任意角三角函数的定义：若已知角α终边与单位圆交于点P(x，y)，则：ysinxcosxytan)0(x2、解题方法总结（1）已知交点P的坐标，直接用定义（2）已知角，则先求交点P的坐标再用定义课本第20页A组题2.xyoP(x,y)αr由相似三角形的知识，对于确定的角α，这三个比值不会随P在α的终边上的位置的改变而改变。MOPPMsinBOBABOPOMcosOAOBOMPMtanOBABA(a,b)α思考：对于一个任意给定的角α，按照上述定义，对应的sinα，cosα，tanα的值是否存在？是否唯一？α的终边P(x，y)Oxy正弦、余弦，正切都是以角为自变量，以单位圆上点的坐标或坐标的比值为函数值的函数，我们将它们统称为三角函数。,sinry,cosrx.tanxy