用向量讨论垂直与平行VIP免费

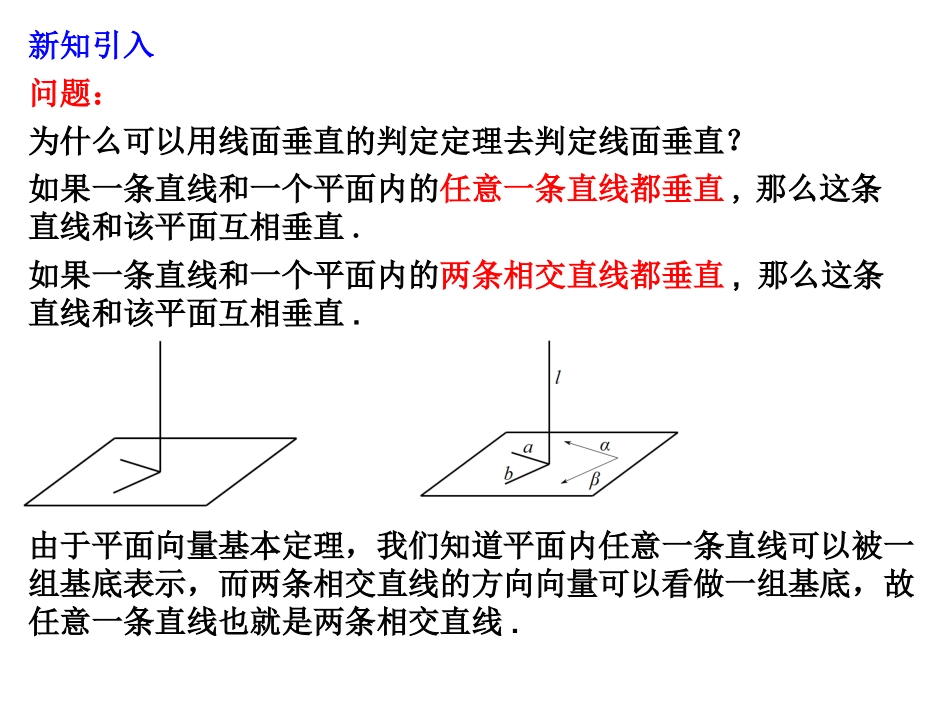
复习回顾1.平面向量基本定理设、是同一平面内的两个不共线的向量,那么对于这一平面内的任意向量,1e2ea2211eea我们把不共线的向量，叫做表示这一平面内所有向量的一组基底.1e2e（2）______________________________;ab0ab1212120xxyyzz（1）若则_______________________________;,0bab//ab121212,,xxyyzz2.空间向量坐标运算的坐标表示12存在唯一一对实数，,使新知引入问题：为什么可以用线面垂直的判定定理去判定线面垂直？如果一条直线和一个平面内的任意一条直线都垂直,那么这条直线和该平面互相垂直.如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线和该平面互相垂直.由于平面向量基本定理，我们知道平面内任意一条直线可以被一组基底表示，而两条相交直线的方向向量可以看做一组基底，故任意一条直线也就是两条相交直线.§4用向量讨论垂直与平行一、垂直问题例1.(线面垂直的判定定理)若一条直线垂直于一个平面内的两条相交直线,则该直线与此平面垂直.mnmnBlmln:,,,,.已知mnlB求证:l.证明:p设p是平面α内任意一条直线,又设直线l,m,n,p的方向向量分别为.,,,pnml由向量共面可得,m,n,ppm+nlplm+n()lm+lnlm,lnlm,ln00lp0lplpp是平面α内任意一条直线l.§4用向量讨论垂直与平行一、垂直问题练习1.如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、D1B1的中点.求证EF⊥平面B1AC.ABDCA1B1C1D1EF证法1:设1,,,ABaADbAAc�则111111122EFEBBFBBBD�1122()cba12()abcACab�2211022()()()EFACababcab�EFAC�同理1EFAB�1,EFACEFAB1ABACAEF⊥平面B1AC.空间的面面垂直线面垂直线线垂直而线线的垂直可化归为向量垂直,即mnabab0练习1.如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、D1B1的中点.求证EF⊥平面B1AC.ABDCA1B1C1D1EF证法2:如图建立空间直角坐标系D-xyz,xyz设正方体的棱长为2，则A(2,0,0),C(0,2,0）B1(2,2,2),E(2,2,1),F(1,1,2)(1,1,1),EF�1(2,2,0),(0,2,2)ACAB�220EFAC�1220EFAB�EFAC1EFAB1ABACAEF⊥平面B1AC.例2.(三垂线定理)若平面内的一条直线垂直于平面外的一条直线在该平面上的投影,则这两条直线垂直.abcn已知：如图,b是平面α外的一条直线,直线c是b在平面α上的投影,条件：直线c与平面内一直线a垂直.求证：a⊥b.证明:过直线b上任意一点作平面α的垂线n，又设直线a,b,c,n的方向向量分别为,,,.abcn由向量共面可得,b,c,nbc+n存在实数λ,µ使得()()abac+anac0ac,anan0an0abab(三垂线定理的逆定理)若平面内的一条直线a垂直于平面外的一条直线b,那么a垂直于直线b在平面上的投影.§4用向量讨论垂直与平行二、平行问题1.线线平行设两直线m,n的方向向量分别是.,bamnmnab//()//或与重合则2.线面平行mnab两个非零向量与平面α共面,一条直线l的一个方向向量为则,abn,lnab//,,llxynxayb或在内存在两个实数使3.面面平行一、垂直问题而线线的垂直可化归为向量垂直,即mnabab0空间的面面垂直线面垂直线线垂直空间的面面平行线面平行线线平行例3.（面面平行判定定理）若一个平面内有两条相交直线都平行于另一个平面,则这两个平面平行.//,,,//,//.ababPab已知：求证：ba2n分析：如图,平面α,β的法向量分别为12,.nn要证α//β,只需证12//.nn证明：设直线a,b的方向向量分别为,.ab//,//ab设平面α,β的法向量分别为12,.nn//,//ab2n22,nanb//ab...