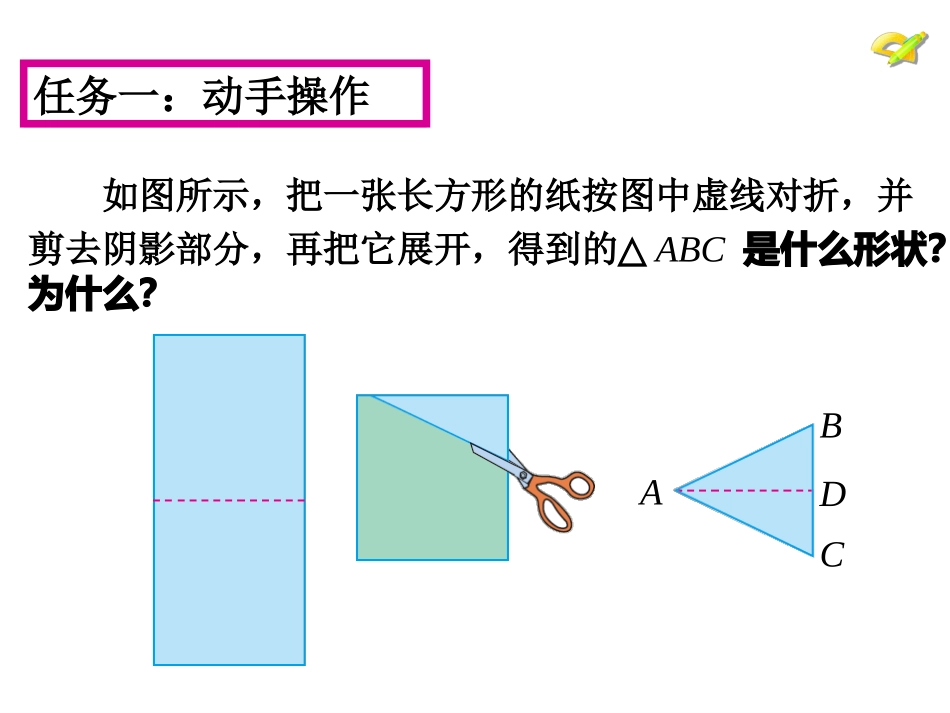
(第一课时)性质如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC是什么形状?为什么?任务一:动手操作ABCD任务二:探索等腰三角形的性质1、把剪出的等腰三角形ABC沿折痕对折,你能发现有哪些重合的线段和角呢?2、由这些重合的线段和角,你能发现等腰三角形的有什么性质?说一说你的猜想。任务三:证明等腰三角形的性质1、等腰三角形的两个底角相等。2、等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合在△ABC中,AB=AC,①∵AD⊥BC,∠=∠,=②∵AD是中线,∴⊥,∠=∠;③∵AD是角平分线,∴⊥,=。ADBC12ADBDBDCD12BDCD⒈等腰三角形一个底角为75°,它的另外两个角为;⒉等腰三角形一个角为70°,它的另外两个角为___________________;⒊等腰三角形一个角为110°,它的另外两个角为________。75°,30°70°,40°或55°,55°35°,35°小试牛刀4、如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。ABCD你的收获让我们来分享习题13.31题,2题,4题10题(选做)如图:在△ABC中,AB=AC,BD=CD.求证:OB=OCDCBAO扩展思维下课了!4、如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。ABCD解:∵AB=AC,BD=BC=AD,∴∠ABC=C=BDC∠∠,∠A=ABD∠(等边对等角)设∠A=x,则∠BDC=A+∠ABD=2x,∠从而∠ABC=C=BDC=2x,∠∠于是在△ABC中,有∠A+ABC+C=x+2x+2x=180°∠∠,解得x=36°,在△ABC中,∠A=36°,∠ABC=C=72°∠x⌒2x⌒2x⌒⌒2x你的细心加你的耐心等于成功!如图:△ABC中,AB=AC,AD和BE是高,它们相交于点H,且AE=BE。求证:AH=2BDABCDEH证明:∵AB=AC,AD是高,BC=2BD∴⌒1⌒2又∵BE是高,∴∠ADC=BEC=AEH∠∠=90°在△AEH和△BEC中∴△AEHBEC(ASA)≌△∴∠1+C=2+C=90°∠∠∠∴1=2∠∠︸∠AEH=BEC∠AE=BE∠1=2∠∴AH=BC∴AH=2BD课后思考一次数学课上,老师布置了一道几何证明题,通过大家的激烈讨论得到了许多种证明方法,聪明的你们,能找出几种证明方法呢?试试看吧!如图,已知△ABC中,AB=AC,F在AC上,在BA的延长线上截取AE=AF,求证:ED⊥BCABCDEF课后思考习题14.3P149D1D4D64、如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。ABCD解:∵AB=AC,BD=BC=AD,∴∠ABC=C=BDC∠∠,∠A=ABD∠(等边对等角)设∠A=x,则∠BDC=A+∠ABD=2x,∠从而∠ABC=C=BDC=2x,∠∠于是在△ABC中,有∠A+ABC+C=x+2x+2x=180°∠∠,解得x=36°,在△ABC中,∠A=36°,∠ABC=C=72°∠x⌒2x⌒2x⌒⌒2x