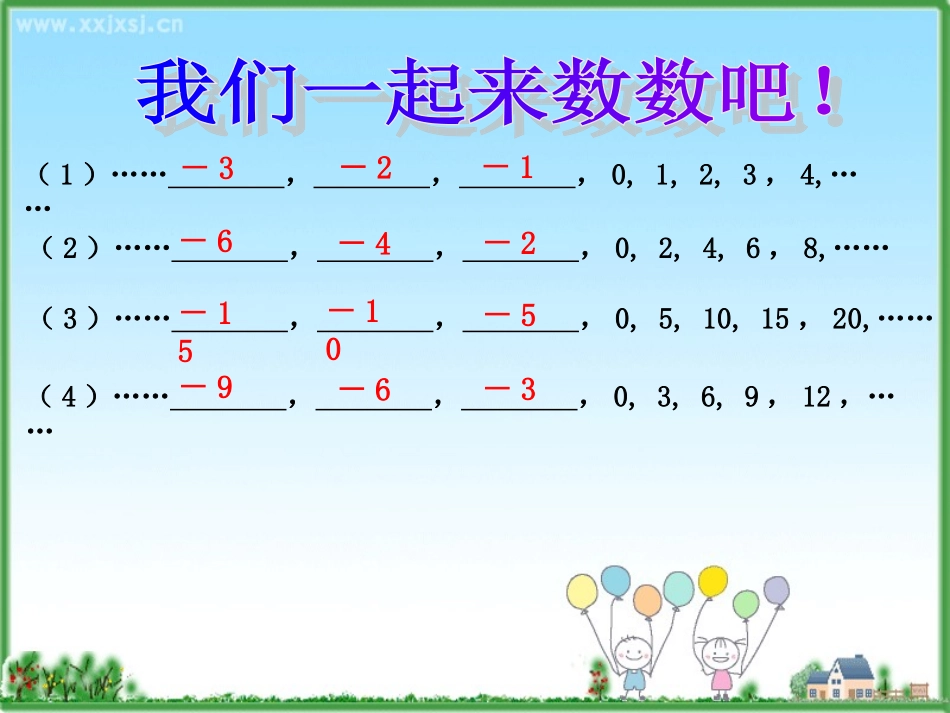
(1)……,,,0,1,2,3,4,……(2)……,,,0,2,4,6,8,……(3)……,,,0,5,10,15,20,……(4)……,,,0,3,6,9,12,……-1-2-3-2-4-6-5-10-15-3-6-9(1)从加法想起;还记得我们在探索有理数的加法法则时,是把有理数的加法划分为几种情况吗?正数+正数负数+负数正数+负数负数+正数正数+0负数+0正数×正数负数×负数正数×负数负数×正数正数×0负数×0√√同号异号(2)探索新知,归纳法则;观察下面的乘法算式,你能发现什么规律吗?3×3=9,3×2=6,3×1=3,3×0=0,3×(-1)=-33×(-2)=-63×(-3)=-9随着后一乘数逐次递减1,积逐次递减3-3-6-93×3=9,2×3=6,1×3=3,0×3=0,(-1)×3=-3(-2)×3=-6(-3)×3=-9随着前一乘数逐次递减1,积逐次递减3-3-6-9正数×正数=正数;正数×负数=负数;负数×正数=负数。积的绝对值等于各乘数绝对值的积。(2)探索新知,归纳法则;观察下面的乘法算式,你能发现什么规律吗?(-3)×3=-9,(-3)×2=-6,(-3)×1=-3,(-3)×0=0,(-3)×(-1)=-3(-3)×(-2)=-6(-3)×(-3)=-9随着后一乘数逐次递减1,积逐次增加3369负数×负数=正数积的绝对值等于各乘数绝对值的积。有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘。任何数与0相乘,都得0.①确定积的符号;②确定积的绝对值。(3)学以致用,加深理解;例1计算:(1)(-3)×9;(2)8×(-1);(3)(-)×(-2).21解:(1)(-3)×9=-27;(2)8×(-1)=-8;(3)(-)×(-2)=1.21课本P30练习1:(1)6×(-9);(2)(-4)×6;(3)(-6)×(-1);(4)(-6)×0;(5)×(-);(6)(-)×.32493141(3)学以致用,加深理解;例2用正负数表示气温的变化量,上升为正,下降为负。登山队攀登一座山峰,每登高1km气温的变化量为-6,℃攀登3km后,气温有什么变化?解:(-6)×3=-18(℃).答:气温下降18.℃课本P30练习2:商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?8×(-1)=-8;5×(-1)=-5;(-7)×(-1)=7;(-2)×(-1)=2;0×(-1)=0;要得到一个数的相反数,只要将它乘-1.-(+8)=-8;-(+5)=-5;-(-7)=7;-(-2)=2;-0=0;在任意一个数前面添上“-”号,新的数就表示原数的相反数。(3)学以致用,加深理解;(3)学以致用,加深理解;×2=1(-)×(-2)=1课本P30练习3:写出下列各数的倒数:1,-1,,-,5,-5,,-。2121乘积是1的两个数互为倒数。31313232正数的倒数是正数,负数的倒数是负数,0没有倒数。倒数等于它本身的数是。±1(4)拓展训练,提高能力;游戏:《我是出题老师》全班按座位分为四个小组,每组发一张白纸,由学生每人各出一道乘法练习或倒数的填空题,(1、2组出乘法练习,3、4组出倒数填空题)。同时,指名两位学生上黑板各出6道题。出题要求:能够快速口答的题目,不得出怪题,所出数字的绝对值不得超过100,可以是整数,也可以是分数、小数。(4)拓展训练,提高能力;1.用“>”,“<”,“=”填空:(1)如果a<0,b<0,那么ab0;(2)如果a>0,b>0,那么ab0(3)如果a>0,b<0,那么ab0(4)如果a=0,b<0,那么ab02.若ab>0,则必有()A.a>0,b>0;B.a<0,b<0;C.a>0,b<0;D.a>0,b>0或a<0,b<0.3.若ab=0,则一定有()A.a=b=0;B.a,b至少有一个为0;C.a=0;D.a,b最多有一个为0.>><=DB(5)归纳小结,形成体系;这节课我学会了什么?(5)布置作业;作业1.必做题:习题1.4第1.2.3题2.选做题:出题给同桌做。