等腰三角形晒课课件VIP免费

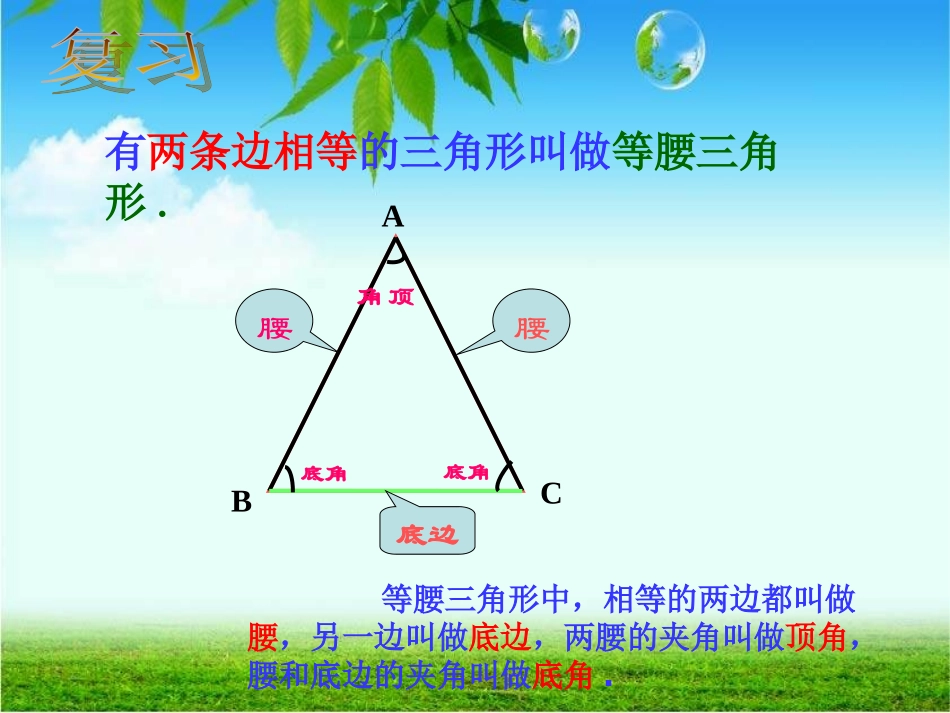
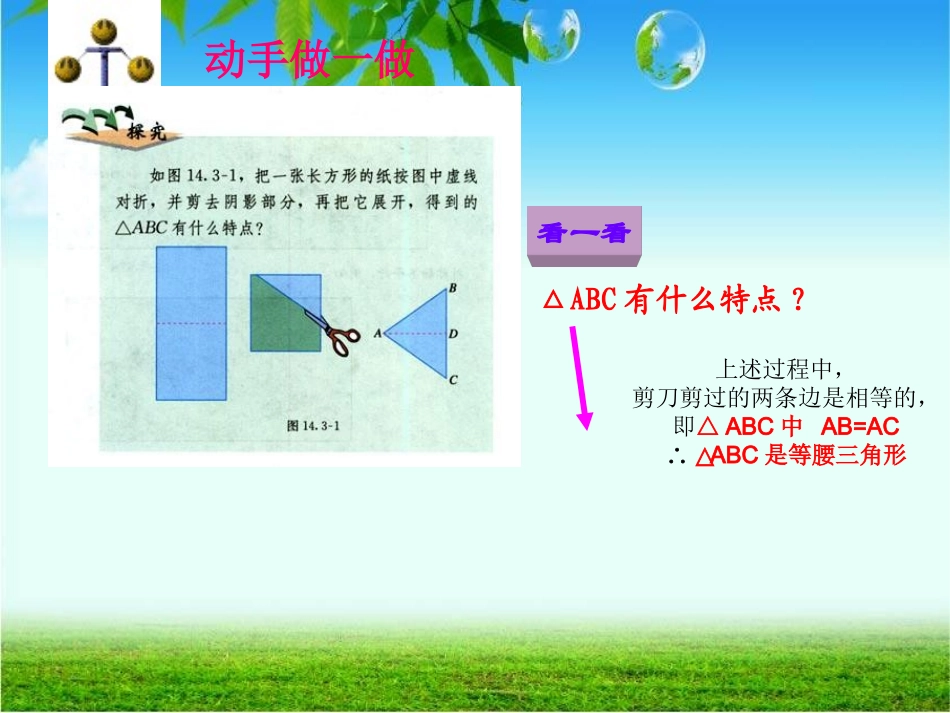
(第一课时)有两条边相等的三角形叫做等腰三角形.等腰三角形中，相等的两边都叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角.ACB腰腰底边顶角底角底角动手做一做△ABC有什么特点?看一看上述过程中，剪刀剪过的两条边是相等的，即△ABC中AB=AC∴△ABC是等腰三角形活动一探究等腰三角形的性质把剪出的等腰三角形ABC沿折痕对折，找出其中重合的线段和角.•由这些重合的线段和角，你能发现等腰三角形的性质吗？说说你的猜想。重合的线段重合的角ACBDAB＝ACBD＝CDAD＝AD∠B＝∠C∠BAD＝∠CAD∠ADB＝∠ADC等腰三角形除了两腰相等以等腰三角形除了两腰相等以外外,,你还能发现它的其他性质吗你还能发现它的其他性质吗??大胆猜想1.2.猜想等腰三角形的两个底角相等。等腰三角形的顶角平分线与底边上的中线，底边上的高互相重合（简称“三线合一”）猜想与论证一：等腰三角形的两个底角相等。已知：△ABC中，AB=AC求证：∠B=C性质1ABCD猜想ABC则有∠1＝∠2D12在△ABD和△ACD中证明:作顶角的平分线AD，AB＝AC∠1＝∠2AD＝AD（公共边）∴△ABD≌△ACD（SAS）∴∠B＝∠C（全等三角形对应角相等）2ABC则有BD＝CDD在△ABD和△ACD中证明:作△ABC的中线ADAB＝ACBD＝CDAD＝AD（公共边）∴△ABD≌△ACD（SSS）∴∠B＝∠C（全等三角形对应角相等）ABC则有∠ADB＝∠ADC＝90ºD在RtABD△和RtACD△中证明:作△ABC的高线ADAB＝ACAD＝AD（公共边）∴Rt△ABD≌Rt△ACD（HL）∴∠B＝∠C（全等三角形对应角相等）等腰三角形性质性质1：等腰三角形两个底角相等，简称“等边对等角”∵AB=AC∴=，数学语言数学语言∠B∠CABC等腰三角形性质2：猜想与论证：ABCD等腰三角形的顶角平分线与底边上的中线，底边上的高互相重合（简称“三线合一”）等腰三角形性质性质2等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。（可简记为“三线合一”）性质2:(1)∵AB=AC，AD是角平分线，∴⊥，____=_____；(2)∵AB=AC，AD是中线，∴⊥，∴∠=∠____；(3)∵AB=AC，AD⊥BC,∴∠_____=∠______，_____=______。BADCADBADCADADBCADBCBDCDBDCD数学语言数学语言等腰三角形是轴对称图形，对称轴是什么？※等腰三角形是轴对称图形，底边上的中线（顶角平分线，顶角平分线，底边上的高））所在的直线所在的直线就是就是它的对称轴它的对称轴。ABPl⒈等腰三角形一个底角为75°,它的另外两个角为_______；⒉等腰三角形一个角为70°,它的另外两个角为___________________；⒊等腰三角形一个角为110°,它的另外两个角为________。75°,30°70°,40°或55°,55°35°,35°活动二运用等腰三角形的性质如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求△ABC各角的度数.ABCD12如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求△ABC各角的度数.∵AD=BD∴∠A=1∠设∠A=x，则∠1=x∵∠2是△ABD的外角∴∠2=A+1∠∠∴∠2=2x∵BD=CD∴∠2=C∠∴∠C=2xABCDx⌒12∵AB=AC∴∠ABC=C∠∴∠ABC=2x在△ABC中∠A+ABC+C=∠∠∴x+2x+2x=180∴x=∴∠A=,∠ABC=∠C=18036367272课堂检测1.在△ABC中，AB=AC．若∠A=50°，则∠B=°，∠C=°；若∠B=45°，则∠A=°，∠C=°；若∠C=60°，则∠A=°，∠B=°；若∠A=∠B，则∠A=°，∠C=°．2.在三角形ABC中，D在BC上，若AD=BD，AB=AC=CD，求角ABC的度数.3.已知如图，在△ABC中，AB=AC，AD是外角∠CAE的平分线．求证：AD∥BC．BCAD谈谈你的收获！等腰三角形是轴对称图形,底边上的中线（顶顶角平分线，角平分线，底边上的高））所在的直线所在的直线就是它的就是它的对称轴对称轴。性质1：等腰三角形两个底角相等，简称“等边对等角”（前提是在同一个三角形中。）性质性质22::等腰三角形的等腰三角形的顶角的顶角平分线、底边上的中线、和底边上的高互相重合，简称“三线合一”（前提是在同一个等腰三角形中。）