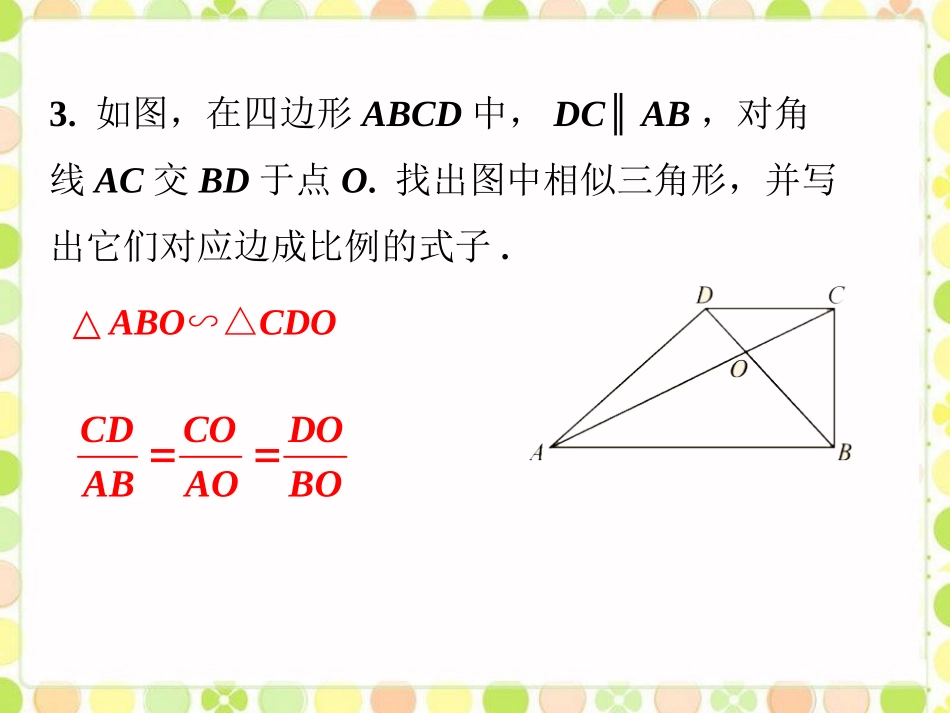
1.已知:在△ABC中,AB=AC;在△A′B′C′中,A′B′=A′C′.(1)如果∠A=∠A′,求证:△ABC∽△A′B′C′;(2)如果∠B=∠B′,求证:△ABC∽△A′B′C′证明:(1)∵AB=AC,∴∠B=∠C=(180°-∠A).(等边对等角)同理,∠B′=∠C′=(180°-∠A)又∵∠A=∠A′,∴∠B=∠B′,∠C=∠C′.∴△ABC∽△A′B′C′.1212(2)∵AB=AC,∴∠B=∠C.(等边对等角)同理,∠B′=∠C′.又∵∠B=∠B′,所以∠C=∠C′.∴△ABC∽△A′B′C′.2.如果△ABC∽△A1B1C1,△A1B1C1∽△A2B2C2,那么△ABC与△A2B2C2有什么关系,为什么?它们相似.∵△ABC∽△A1B1C1,∴这两个三角形的三个对应角相等.又∵△A1B1C1∽△A2B2C2,∴△A1B1C1与△A2B2C2对应的三个角相等,则△ABC与△A2B2C2对应角相等,故△ABC∽△A2B2C2.3.如图,在四边形ABCD中,DC∥AB,对角线AC交BD于点O.找出图中相似三角形,并写出它们对应边成比例的式子.△ABO∽△CDOCDCODOABAOBO