《解直角三角形》课件VIP免费

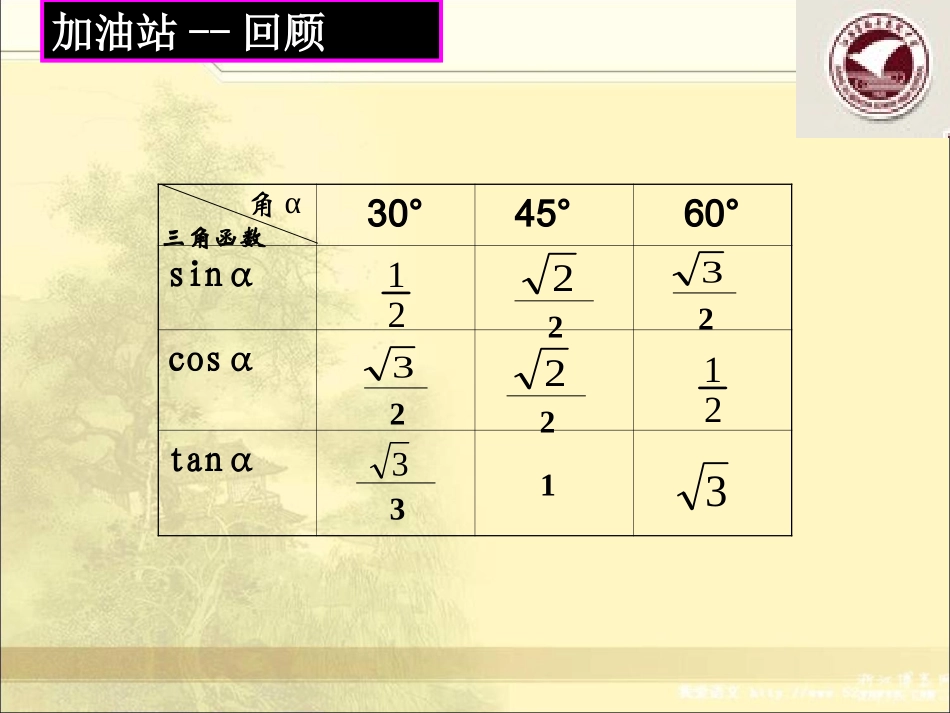
聪明在于学习，天才在于积累。……所谓天才，实际上是依靠学习。---------华罗庚28.2.1解直角三角形饶河县第二中学薛怀杰加油站--回顾30°45°60°sinαcosαtanα角α三角函数21222221323231332.过程与方法目标：经历观察、猜想等用数学方法解决问题的过程，感知“数形结合”的思想方法。3.情感目标：“严谨”和“积极”4.目标解析：达成目标（1）的标志是：知道解直角三角形的内涵，以及根据直角三角形中已知元素，明确所有要求的未知元素；根据已知条件，能从全等三角形判定定理的角度，判断是否能解直角三角形。达成目标（2）的标志是：根据元素间的关系，选择适当关系式，求出所有未知元素。5.学习难点：恰当选择锐角三角函数，把已知与未知联系起来。1.知识与技能目标：（1）了解解直角三角形的意义和条件；（2）能根据直角三角形中除直角以外的两个元素（至少有一个是边），解直角三角形。多项创设情境揭示课题如图设塔顶中心点为B，塔身中心线与垂直中心线的夹角为A，过B点向垂直中心线引垂线，垂足为点C，在Rt△ABC中，∠C＝90°，BC＝5.2m，AB＝54.5m利用计算器可得.根据以上条件可以求出塔身中心线与垂直中心线的夹角．你愿意试着计算一下吗？ABC0954.05.542.5sinABBCAA528将上述问题推广到一般情形，就是：已知直角三角形的斜边和一条直角边，求它的锐角的度数.新知识新知识在直角三角形中,由已知元素求其余未知元素的过程,叫解直角三角形合作探究一1.一个直角三角形（除直角外）有几个元素？它们之间有何关系？2.知道元素中的几个，就可以求其他元素？ＡＣＢabc展示题目展示组质疑组1五组一组2（1）三组二组2（2）二组三组3（3）一组四组3（4）四组五组合作探究一1.一个直角三角形（除直角外）有几个元素？它们之间有何关系？2.知道元素中的几个，就可以求其他元素？(1)三边之间的关系:a2＋b2＝c2（勾股定理）；(2)锐角之间的关系:∠A＋∠B＝90º；(3)边角之间的关系:sinA＝accosA＝tanA＝除直角外，有5个元素，即有三条边和两个角，ＡＣＢabcbcab锐角三角函数合作探究一在RtABC△中,不能不能一角一角一边ABC两角（2）根据∠A=60°,∠B=30°,你能求出这个三角形的其他元素吗?（1）根据∠A=60°，你能求出这个三角形的其他元素吗?（3）根据∠A=60°,斜边AB=4,你能求出这个三角形的其他元素吗?（4）根据BC=2，AC=2，你能求出这个三角形的其他元素吗？3∠B=30°AC=2BC=2两边∠A∠BAB（4）根据BC=2，AC=2，你能求出这个三角形的其他元素吗？3四合作探究一小结在RtABC△中,(其中至少有一个是边),在直角三角形的六个元素中,除直角外,如果知道两个元素,就可以求出其余三个元素.我发现了：一角一边两边两角不能求其它元素一角能求其它元素ABCDFE由直角三角形的判定定理可知：对于直角三角形，如果已知除直角外的两个元素分别相等（其中至少有一个是边），那么这两个三角形全等。从而一个直角三角形的大小由三边和两个锐角中的两个元素（其中至少有一个是边）唯一确定，因此，我们就可以利用一边和另一个元素求其余元素。四合作探究一小结合作探究二解直角三角形例1:在RtABC△中,C=90°,AC=,BC=,∠解这个直角三角形.ABC6226试一试你学会了吗？如图，在Rt△ABC中，∠C＝90°，a=20,b=20,解这个直角三角形.3a=20b=203ABC合作探究二解直角三角形例2：在RtABC△中,C=90°,B=35°,b=20,∠∠解这个直角三角形.(精确到0.1)ＡＣＢabc尽量选择原始数据,避免累积错误35°20？？？在RtABC,C=90°,A=45°,c=4△∠∠解这个直角三角形.CBA45°C=4解： ∠A=45°∴∠B=90°—A=45°,∠sinA＝ac a＝sinA·c=sin45°·4=·4=2222∴cosA＝bc b＝cosA·c=cos45°·4=·4=2222∴ab也可以： ∠A=B=45°∠∴b=a=22试一试你学会了吗？建模应用1.自编一道解直角三角形的题并解答。2.独立完成后，小组交流。3.小组代表展示。建模应用第一类：已知直角三角形的一个锐角和这个锐角的对边，解这个直角三角形。第二类：已知直角三角形的一个锐角和这个锐角的邻边，解这个直角三角形。第三类：已知直角三角形的一个锐角和这个锐角的斜边，解这个直角三角形。第四类：已知直角三角形的两条直...