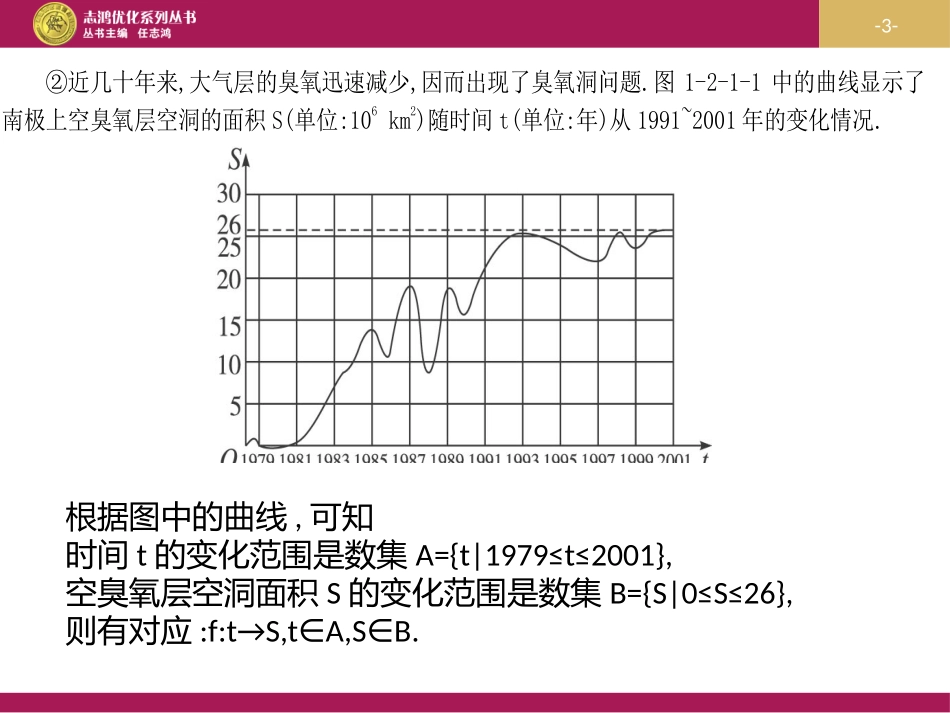
1.2.1函数的概念(第一课时)-2-问题1:给出下列三种对应:①一枚炮弹发射后,经过26s落到地面击中目标.炮弹的射高为845m,且炮弹距地面的高度为h(单位:m)随时间t(单位:s)变化的规律是h=130t-5t2.时间t的变化范围是数集A={t|0≤t≤26},h的变化范围是数集B={h|0≤h≤845}.则有对应f:t→h=130t-5t2,tA,hB.∈∈-3-②近几十年来,大气层的臭氧迅速减少,因而出现了臭氧洞问题.图1-2-1-1中的曲线显示了南极上空臭氧层空洞的面积S(单位:106km2)随时间t(单位:年)从1991~2001年的变化情况.根据图中的曲线,可知时间t的变化范围是数集A={t|1979≤t≤2001},空臭氧层空洞面积S的变化范围是数集B={S|0≤S≤26},则有对应:f:t→S,t∈A,S∈B.根据图中的曲线,可知时间t的变化范围是数集A={t|1979≤t≤2001},空臭氧层空洞面积S的变化范围是数集B={S|0≤S≤26},则有对应:f:t→S,tA,SB.∈∈-4-③国际上常用恩格尔系数反映一个国家人民生活质量的高低,恩格尔系数越低,生活质量越高.下表中的恩格尔系数y随时间t(年)变化的情况表明,“八五”计划以来,我国城镇居民的生活质量发生了显著变化.“八五”计划以来我国城镇居民恩格尔系数变化情况时间19911992199319941995199619971998199920002001恩格尔系数y53.852.950.149.949.948.646.444.541.939.237.9根据上表,可知时间t的变化范围是数集A={t|1991≤t≤2001},恩格尔系数y的变化范围是数集B={S|37.9≤S≤53.8}.则有对应:f:t→y,t∈A,y∈B.请同学们思考以上三个对应有什么共同特点?根据上表,可知时间t的变化范围是数集A={t|1991≤t≤2001},恩格尔系数y的变化范围是数集B={S|37.9≤S≤53.8}.则有对应f:t→y,tA,yB.∈∈请同学们思考以上三个对应有什么共同特点?以上三个对应的共同特点:(1)集合A、B都是非空数集;(2)两个数集间都有一种确定的对应关系;(3)对于数集A中的每一个元素x,在对应关系f:A→B下,在数集B中都有唯一确定的元素y与之对应.-5-一、函数的定义:一般地,设A、B都是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记y=f(x),xA,∈其中x叫自变量。x的取值范围A叫做函数的定义域,函数值的集合{f(x)|xA}∈叫做函数的值域.-6-自主输入运算加工输出结果生活中的”函数”现象rwrq-7-自变量x运算f(x)因变量y问:初中函数与高中函数的区别表示方法不一样了13xy1x2113y13xxf13xxfy-8-例1:判断下列对应关系是否为集合A到集合B的函数:.0:;0,1,1)2(;:,0,)1(yxfBAxyxfxxBRA-9-二.函数的三要素1.定义域函数的定义域就是自变量x的取值范围,如果未加特殊说明,函数的定义域就是能使表达函数的式子各部分都有意义的所有实数的x的取值,实际问题中,必须考虑自变量x所代表的具体的量的实际取值范围,例如的定义域为{x|x不为0}。xy1-10-例2.求函数y=xxx11)1(2的定义域.答案:{x|x≤1,且x≠-1}.-11-*求定义域的一般法则:,即交集。都有意义的实数的集合数学式子它的定义域是使各部分的函数,由几部分数学式子构成中)()分式分母不为零;(大于等于零;偶次根号下的被开方数;实数集为整式,则其定义域为)若()5(;043)2(R10aaxf-12-2.对应关系对应关系f是核心,它是对自变量进行“操作”的“程序”或者“方法”,是连接x与y的纽带,按照这一“程序”,从定义域集合A中任取一个x,可得到值域{y=f(x)且xA}中唯一确定的y与之对应。-13-3.值域函数的值域是函数值的集合,通常一个函数的定义域和对应关系确定了,那么它的值域也随之确定。总结:如果两个函数的定义域相同,并且对应关系一致,那么我们就称这两个函数相等。问题:函数f:A→B的值域为C,那么集合B=C吗?BC不相等,-14-思考:下列各组式子是否表示同一函数:.,)2(;,)1(222xxgxxfttxxf-15-定义名称符号数轴表示{x|a≤x≤b}闭区间[a,b]{x|a
a}(a,b]{x|x≤a}(-∞,a]{x|x