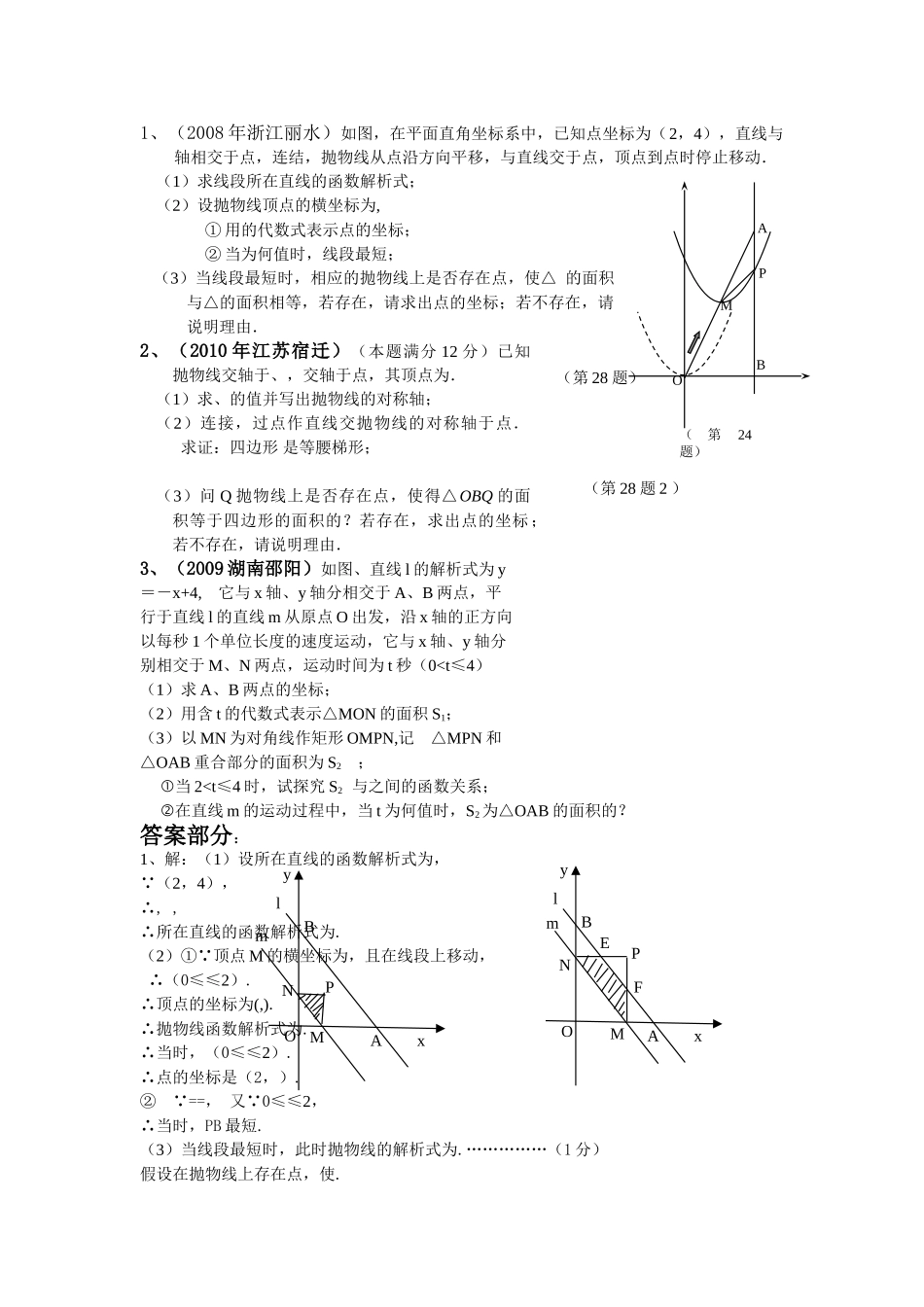
中考数学专题----面积问题(2)面积倍分问题面积问题在中考中占有很重要的地位,一般情况下,计算一些基本图形的面积,可以直接运用图形的面积公式,对于一些不规则的图形面积的计算,可以对图形进行转化,这类问题虽然解题方法比较灵活多样,但难度一般不太大。但是,在中考压轴题中,有关面积的问题常常以动态的方式出现,经常与函数知识联系起来,有时还需要分类讨论。因此,对考生要求较高,在解题时,要注意分清其中的变量和不变量,并把运动的过程转化成静止的状态,做到动静结合,以静求动。中考数学面积问题的考点主要有:(1)面积的函数关系式问题;(2)面积的最值问题;(3)面积的倍分问题。前二个考点在上次的专题中已经讲过,今天我们来探究面积的倍分问题。一、典型例题:1、(2007江苏扬州)如图,矩形中,厘米,厘米().动点同时从点出发,分别沿,运动,速度是厘米/秒.过作直线垂直于,分别交,于.当点到达终点时,点也随之停止运动.设运动时间为秒.(1)若厘米,秒,则______厘米;(2)若厘米,求时间,使,并求出它们的相似比;(3)若在运动过程中,存在某时刻使梯形与梯形的面积相等,求的取值范围;(4)是否存在这样的矩形:在运动过程中,存在某时刻使梯形,梯形,梯形的面积都相等?若存在,求的值;若不存在,请说明理由.分析:问题(1)比较容易解答,问题(2)利用三角形相似的性质也容易解决,问题(3)需要利用BM=BN=t,利用面积相等求出t和a的关系式,利用t的范围求a的取值范围,问题(4)只需要在问题(3)的基础上,让梯形PQCN的面积与梯形PMBN的面积相等即可。解.(1),(2),使,相似比为(3),,即,当梯形与梯形的面积相等,即化简得,,,则,(4)时,梯形与梯形的面积相等梯形的面积与梯形的面积相等即可,则,把代入,解之得,所以.所以,存在,当时梯形与梯形的面积、梯形的面积相等.温馨提示:本题考查与面积有关的问题,解答的关键是将梯形的面积相等转化后求解,另外,在解决这一类问题时,要善于运用数形结合的思想,把几何条件转化,建立合适的数学模型,本题就充分运用了方程的思想。二、名题精练:DQCPNBMADQCPNBMA1、(2008年浙江丽水)如图,在平面直角坐标系中,已知点坐标为(2,4),直线与轴相交于点,连结,抛物线从点沿方向平移,与直线交于点,顶点到点时停止移动.(1)求线段所在直线的函数解析式;(2)设抛物线顶点的横坐标为,①用的代数式表示点的坐标;②当为何值时,线段最短;(3)当线段最短时,相应的抛物线上是否存在点,使△的面积与△的面积相等,若存在,请求出点的坐标;若不存在,请说明理由.2、(2010年江苏宿迁)(本题满分12分)已知抛物线交轴于、,交轴于点,其顶点为.(1)求、的值并写出抛物线的对称轴;(2)连接,过点作直线交抛物线的对称轴于点.求证:四边形是等腰梯形;(3)问Q抛物线上是否存在点,使得△OBQ的面积等于四边形的面积的?若存在,求出点的坐标;若不存在,请说明理由.3、(2009湖南邵阳)如图、直线l的解析式为y=-x+4,它与x轴、y轴分相交于A、B两点,平行于直线l的直线m从原点O出发,沿x轴的正方向以每秒1个单位长度的速度运动,它与x轴、y轴分别相交于M、N两点,运动时间为t秒(0