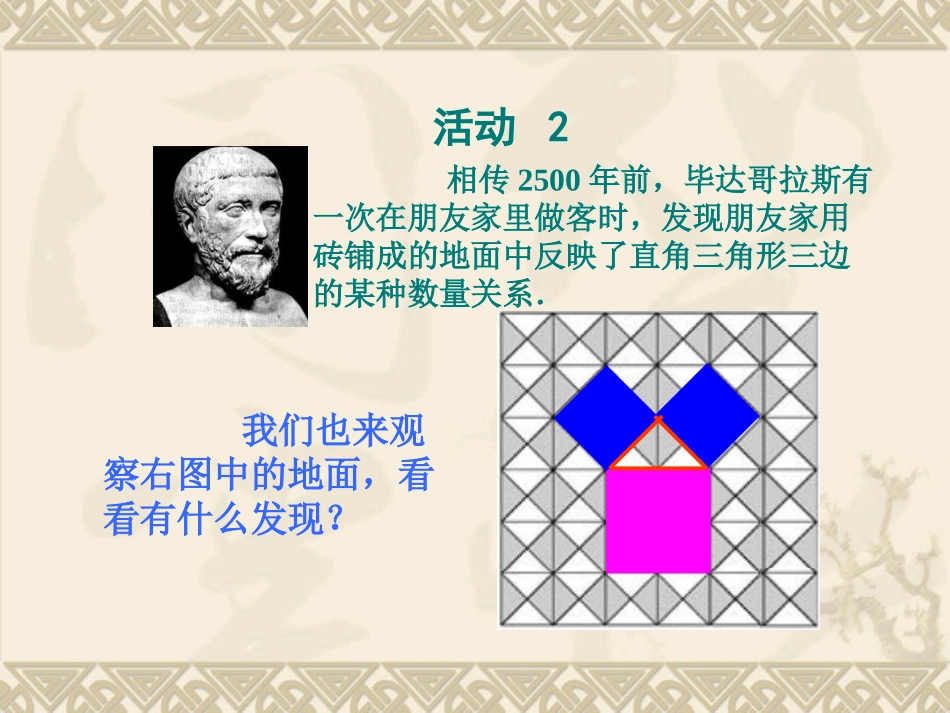
这就是本届大会会徽的图案.活动1这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”.18.1勾股定理—1活动2相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.我们也来观察右图中的地面,看看有什么发现?1.观察图1-1(图中每个小方格代表一个单位面积)ABC图1-1正方形A中含有个小方格,即A的面积是个单位面积.正方形B的面积是个单位面积.正方形C的面积是个单位面积.9918你是怎样得到上面的结果的?与同伴交流交流.1239继续图1-1CS正方形1433182分割成若干个直角边为整数的三角形返回CABCS正方形216218把C看成边长为6的正方形面积的一半CAB图1-1返回ABC图1-2ABC图1-32.观察右边两个图并填写下表:A的面积B的面积C的面积图1-2图1-3169254913你是怎样得到表中的结果的?与同伴交流交流.做一做ABC图1-2ABC图1-33.三个正方形A,B,C面积之间有什么关系?SA+SB=SC即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.议一议ABC图1-2ABC图1-34.你能发现直角三角形三边长度之间存在什么关系吗?与同伴交流.bac222abc直角三角形两直角边的平方和等于斜边的平方.abc是不是所有的直角三角形都具有这样的特点呢?这就需要我们对一个一般的直角三角形进行证明.到目前为止,对这个命题的证明方法已有几百种之多.下面我们就来看一看我国数学家赵爽是怎样证明这个命题的.结论cba(b-a)2中黄实朱实活动3看左边的图案,这个图案是公元3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形(黄色).赵爽弦图的证法224()42SSSabcba大正方形小正方形直角三角形化简得:c2=a2+b2.cba(b-a)2中黄实朱实勾股定理如果直角三角形两直角边分别为a、b,斜边为c,那么222abc直角三角形两直角边的平方和等于斜边的平方.abc结论变形c2=a2+b2abcABC如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上的一点,测得CB=60m,AC=20m,你能求出A、B两点间的距离吗?(结果保留整数)例(1)求出下列直角三角形中未知的边.610ACB8A15CB练习30°2245°ABBACC(2)一个门框尺寸如下图所示.①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过?②若薄木板长3米,宽1.5米呢?③若薄木板长3米,宽2.2米呢?为什么?ABC1m2m∵木板的宽2.2米大于1米,∴横着不能从门框通过;∵木板的宽2.2米大于2米,∴竖着也不能从门框通过.∴只能试试斜着能否通过,对角线AC的长最大,因此需要求出AC的长,怎样求呢?(4)如图,一个3米长的梯子AB,斜着靠在竖直的墙AO上,这时AO的距离为2.5米.①求梯子的底端B距墙角O多少米?②如果梯子的顶端A沿墙角下滑0.5米至C,请同学们:猜一猜,底端也将滑动0.5米吗?算一算,底端滑动的距离近似值是多少?(结果保留两位小数)BDCOA小结:小结:布置作业:布置作业:11、勾股定理的证明、勾股定理的证明22、勾股定理的应用、勾股定理的应用11、教材、教材6969页页11题、题、7070页页22题题22、收集有关勾股定理的证明方法,下节课展示、、收集有关勾股定理的证明方法,下节课展示、交流.交流.