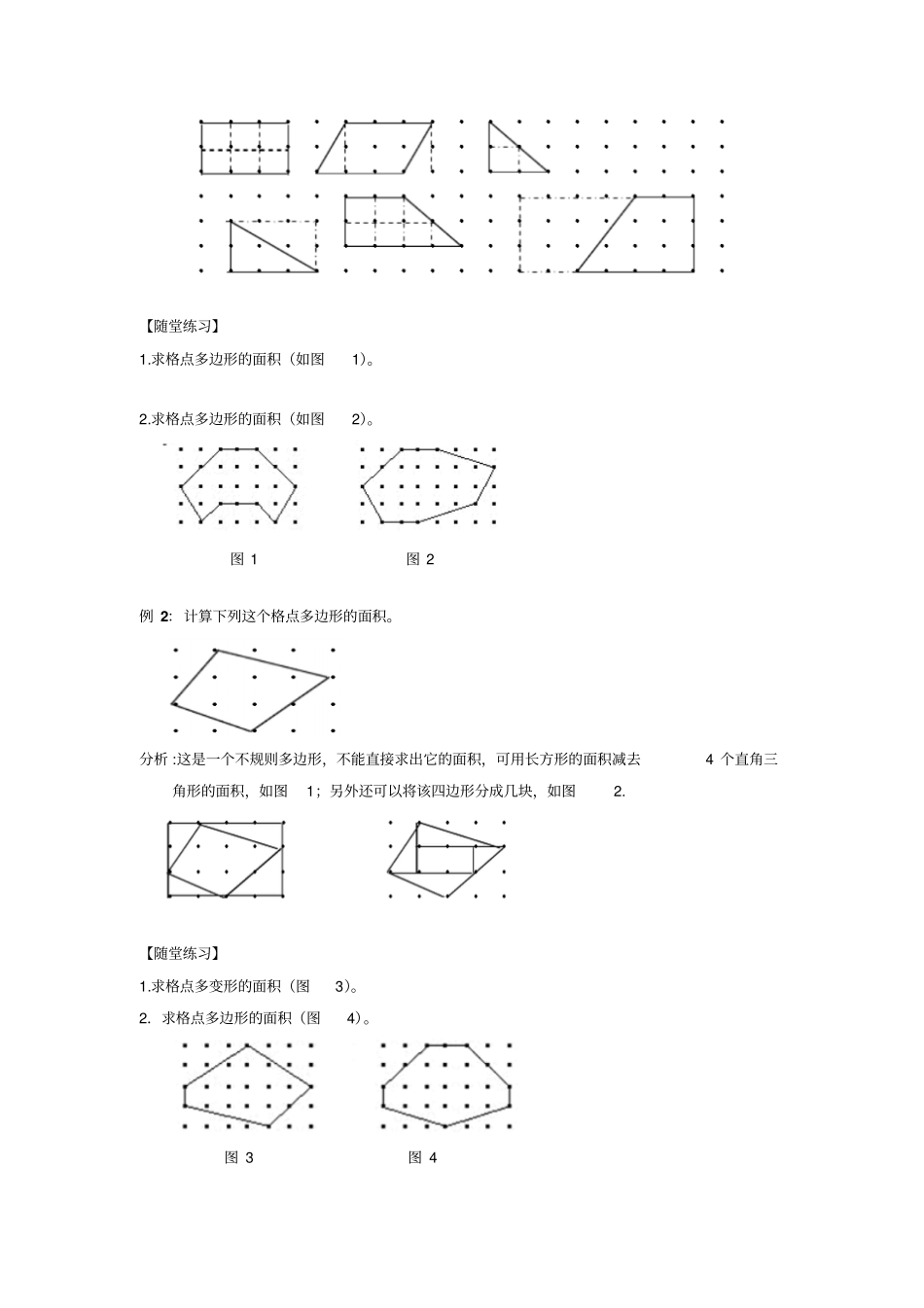
这一讲我们主要介绍利用格点求几何图形的面积,先来介绍什么叫“格点”。见右图:这是一张由水平线和垂直线组成的方格纸,我们把水平线和垂直线相交的点称为“格点”,水平线和垂直线围成的每个小正方形称为“面积单位”。借助小格点,我们可以很快地比较和计算图形的面积大小。利用格点求图形的面积有两种思路,一是直接将图形分成若干个面积单位,然后通过计算有多少个面积单位来求图形的面积;二是将某些图形转化成长方形的面积来求。当然还可以将这两种方法结合起来,求出某些较复杂图形的面积。格点面积公式=中间格点数+图形一周的格点数÷2﹢1【典型例题】例1:计算下列各图的面积。分析:先仔细观察图中的每个图形,选择方法,显然第一、三、五图可以直接数出包含多少个面积单位,而二、四、六显然不适合用数单位面积的方法来求面积,可以采用虚线把这些图形扩展或割补成长方形,通过求长方形的面积来求这些图形的面积。解:(1)图中长方形的面积包括了3×2=6(个)面积单位,所以它的面积为6个面积单位。(2)将图中的平行四边形割补成一个长方形,长方形的面积为3×2=6,而平行四边形的面积等于长方形的面积,所以平行四边形的面积是3×2=6(个)面积单位。(3)将图中三角形用虚线分成3块,它包含1个单位面积和2个单位面积的一半,合起来有2个面积单位,所以它的面积是2个面积单位。(4)图中三角形扩展成一个长方形,长方形的面积为3×2=6,而三角形面积为长方形面积的一半,则三角形面积为3个面积单位。(5)将图中梯形用虚线分成3块,它包含了有5个单位面积和2个单位面积的一半。合起来有6个面积单位。所以它的面积为6个面积单位。(6)将图中梯形互相平行的一组对边延长,补出一个与原来梯形方向颠倒,但面积一样的梯形,形成一个大的长方形。长方形面积为(2+4)×3=18,而梯形的面积为长方形面积的一半,所以梯形的面积是(2+4)×3÷2=9(个)面积单位。【随堂练习】1.求格点多边形的面积(如图1)。2.求格点多边形的面积(如图2)。图1图2例2:计算下列这个格点多边形的面积。分析:这是一个不规则多边形,不能直接求出它的面积,可用长方形的面积减去4个直角三角形的面积,如图1;另外还可以将该四边形分成几块,如图2.【随堂练习】1.求格点多变形的面积(图3)。2.求格点多边形的面积(图4)。图3图4例3:相邻四点连成的小正方形面积是1平方厘米。分别连接各点,组成下列12个图形,你发现有什么排列规律?分析:横看,从左到右图形一周的格点数逐渐增多,中间的格点数保持不变。竖看,从上往下图形一周的格点数保持不变,中间的格点数逐渐增多。图形一周的格点数,中间的格点数与面积究竟有什么关系呢?我们可以将图形按中间没有格点,中间有一个格点和中间有两个格点进行分组列表分析。第一组图形编号①②③④一周格点数46814中间格点数0000面积(平方厘米)1236中间没有格点时,面积=一周格点数÷2-1第二组图形编号⑤⑥⑦⑧一周格点数46811中间格点数1111面积(平方厘米)2347中间有一个格点时,面积=1+一周格点数÷2-1第三组图形编号⑨⑩⑾⑿一周格点数46814中间格点数2222面积(平方厘米)3488中间有2个格点时,面积=2+一周格点数÷2-1解:(1)中间格点数相同时,图形的面积随着一周的格点数增加而增加;当一周的格点数相同时,图形的面积随着中间的格点数增加而增加。(2)各图形面积(见上表)的大小与一周的格点数,中间的格点数都有关系,格点图形面积的计算公式是:图形的面积=中间格点数+图形一周的格点数÷2-1【随堂练习】1.通过割补图形求格点多边形的面积(图5)。2.通过割补法求格点多边形的面积(图6)。3.利用格点多边形面积公式计算,结果一样吗?图5图6例4:下图中的每一个小正方形的面积都是4平方厘米,求图中阴影部分的面积。分析:内部格点数为9个,周界上格点数为8个,根据格点面积公式可求出阴影部分的面积为:解:4×(9+8÷2﹣1)=48(平方厘米)【随堂练习】1.求格点图形面积(图7)。2.求格点图形面积(图8)。例5:在下面图中有21个点,每相邻三点构成一个单位面积的等边三角形,计算三角形ABC的面积。分...