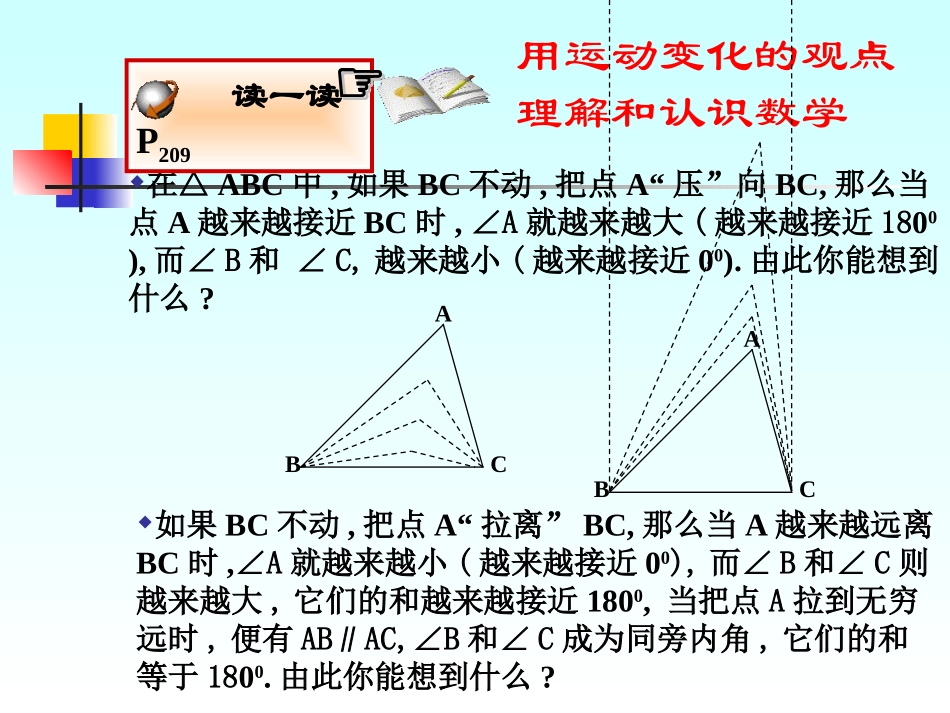
三角形内角和定理的证明授课人:宁一凡兰州市第十一中学用运动变化的观点理解和认识数学在△ABC中,如果BC不动,把点A“压”向BC,那么当点A越来越接近BC时,∠A就越来越大(越来越接近1800),而∠B和∠C,越来越小(越来越接近00).由此你能想到什么?如果BC不动,把点A“拉离”BC,那么当A越来越远离BC时,∠A就越来越小(越来越接近00),而∠B和∠C则越来越大,它们的和越来越接近1800,当把点A拉到无穷远时,便有AB∥AC,∠B和∠C成为同旁内角,它们的和等于1800.由此你能想到什么?读一读P209☞☞CBACBA实验一(折叠):先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行(图1),然后把另处两角相向对折,使其顶点与已折角的顶点相嵌合(图2)、(图3),最后得到(图4)所示的结果。ACB图1BAC图2BAC图3BAC图4实验二(搬移)将纸片三角形顶角剪下,随意将它们拼凑在一起。三角形的三个内角和等于180°结论分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.你还有其它方法来证明三角形内角和定理吗?.ABCD213E方法一一题多解由此你受到什么启发?证明:过点A作PQBC,∥则ABC∠1=B(∠两直线平行,内错角相等),∠2=C(∠两直线平行,内错角相等),又∵∠1+2+∠∠3=1800(平角的定义),∴∠BAC+B+∠∠C=1800(等量代换).PQ231方法二我们证明了三角形内角和定理。证明的基本思想是:运用辅助线将原三角形中处于不同位置的三个内角集中在一起,拼成一个平角,辅助线是联系命题的条件和结论的桥梁,今后我们还要学习它。小结拓展小结:本节课你有什么收获?(1)ABCPRQPTSN(2)ABCQRMTSN(3)ABCPQRM联系与拓广:是否可以把三角形的三个角“凑”到边上的一点P呢?(如图(1))如果把三个角“凑”到三角形内一点呢?(如图(2))“凑”到三角形外一点呢?(如图(3))·课后作业习题6.61,2,3下课了!