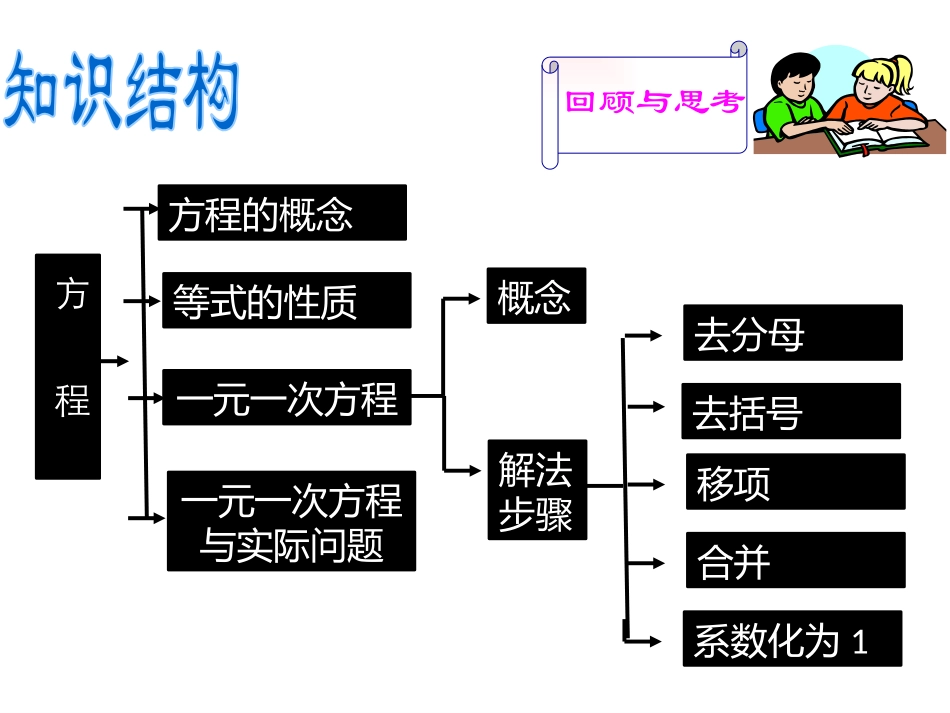
回顾与思考方程概念解法步骤去括号移项合并去分母系数化为1等式的性质方程的概念一元一次方程一元一次方程与实际问题1.什么是一元一次方程?想一想只有一个未知数一元一次方程未知数的次数为1分母不含有字母第1、11题等式性质有哪些?并以字母的形式表示出来等式性质1:如果a=b,那么a+c=b+c需注意的是“同一个数,或同一个式子”。等式性质2:如果a=b,那么ac=bc(c0)需注意的是“两边都乘,不要漏乘”;“同除一个非0的数”想一想1、第4题2、已知x=y,下列变形中不一定正确的是()A.x-5=y-5B.-3x=-3yC.mx=myD.22xyccD变形名称注意事项去分母去括号移项合并(ax=b)系数化成1防止漏乘(尤其整数项),注意添括号;注意变号,防止漏乘;移项要变号,计算要仔细,不要出差错;计算要仔细,分子分母不要颠倒解一元一次方程解:由题意得去分母得11[5(x+1)-4]+8(7x-1)=0(等式性质2)去括号得11[5x+1]+56x-8=0(乘法分配律)55x+11+56x-8=0移项得55x+56x=8-11(等式性质1)合并同类项得111x=-3(乘法分配律)系数化为1得x=(等式性质2)例2:某超市推出如下优惠方案:①一次性购物不超过100元,不享受优惠;一次性❷购物超过100元但不超过300元,一律九折:一次性购物超过❸300元,一律八折。王波两次购物分别付款80元和252元,如果他一次性购买,则应付款多少元?思考:1、享受九折优惠实付款范围是多少?2、享受8折优惠实付款的范围是多少?3、因为王波第一次购物实付款是元,所以是按方案付款。4、王波第二次购物实付款元,所以他是按哪种方案付款的?大于90小于或等于270大于24080①252可能是方案也可能是方案❷❸解:设王波第二次购物付款252元的商品的标价为x元。因为252<30090%,且252>30080%,所以购物付款252元的商品的标价可能超过300元,也可能未超过300元,应分两种情况讨论:(1)未超过300元时,有90%x=252,解得x=280(2)超过300元时,有80%x=252,解得x=315所以两次购物商品的标价是280+80=360(元)或315+80=395(元)36080%=288(元)39580%=316(元)答:他一次购买应付款288元或316元。