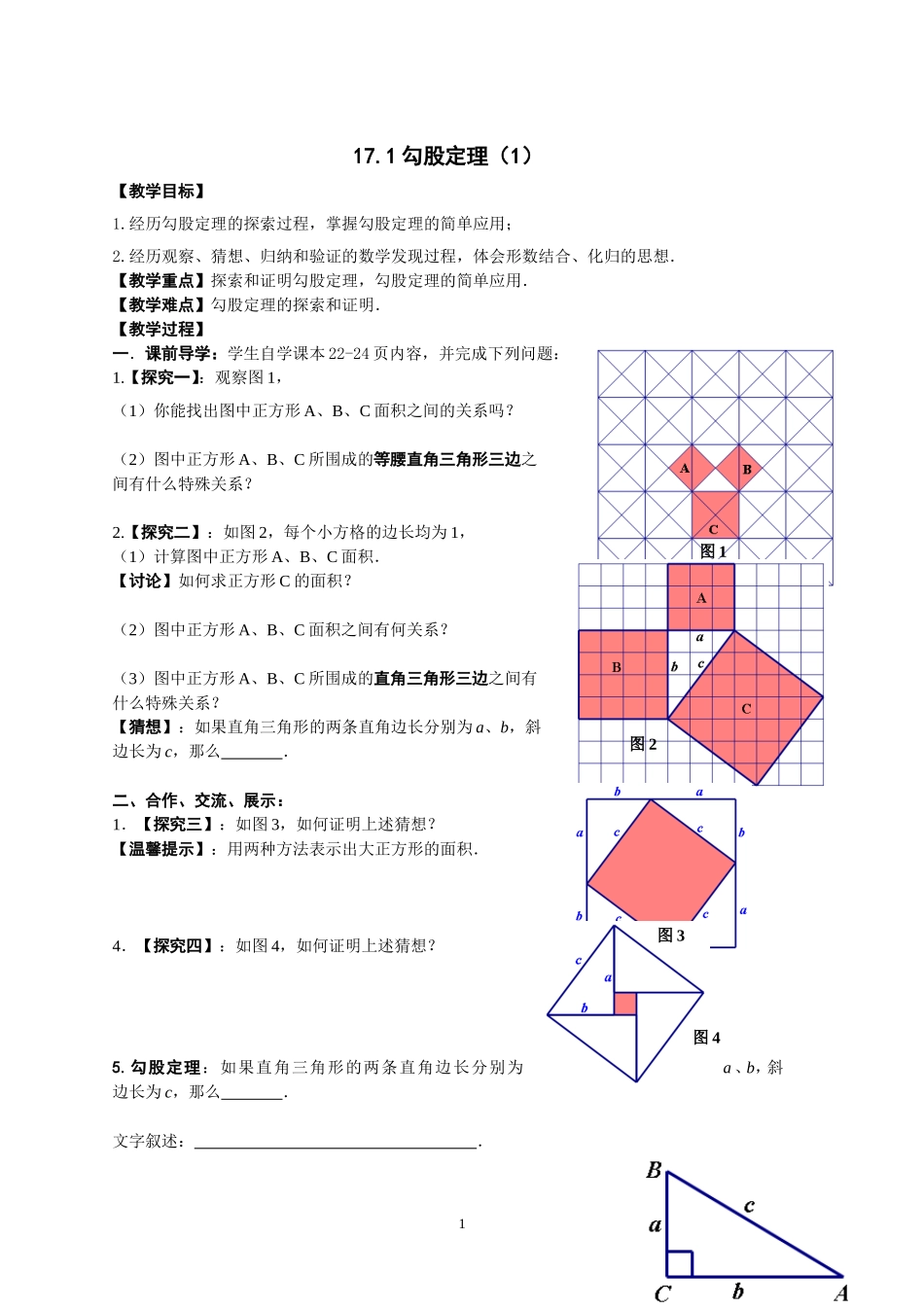
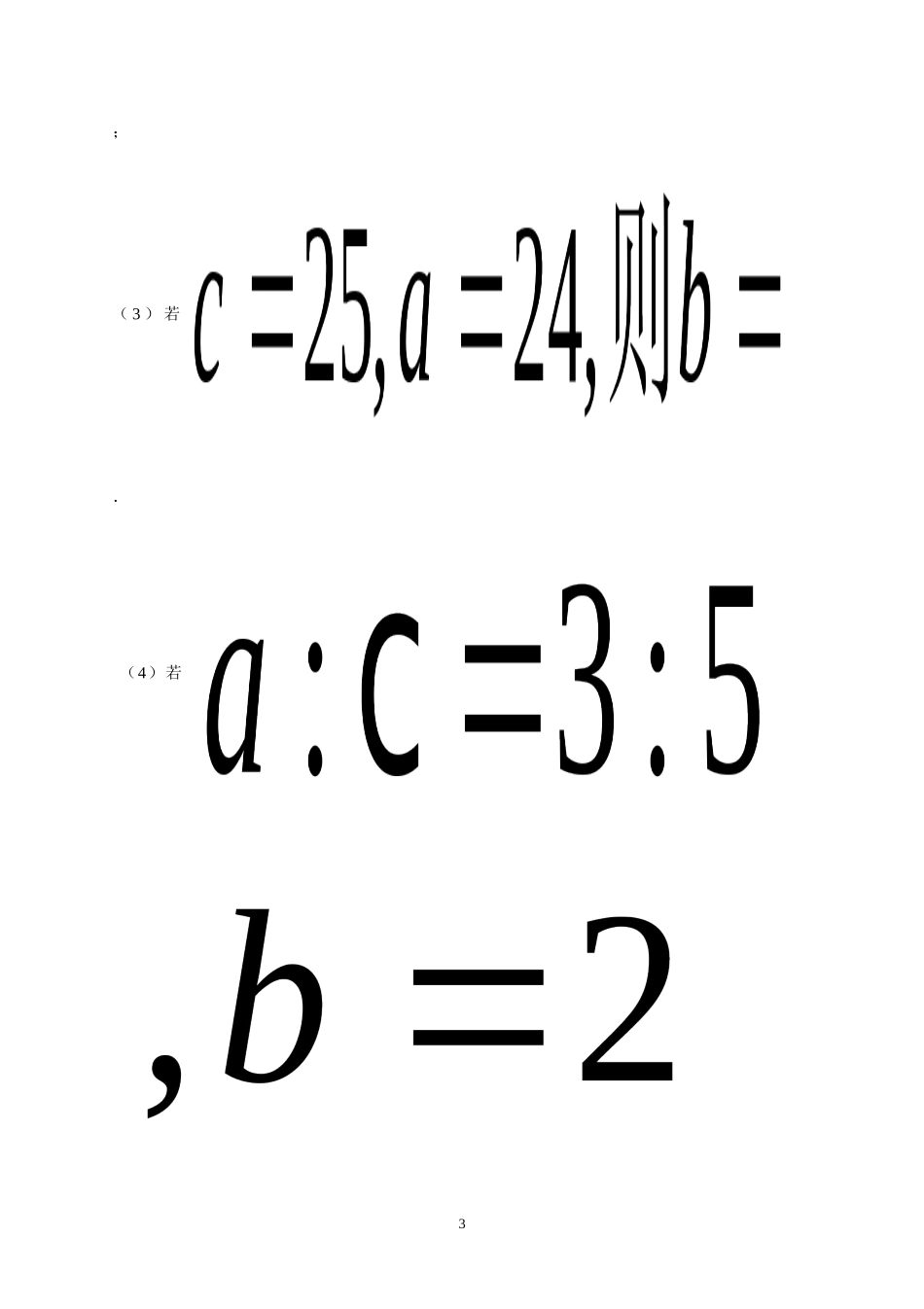17.1勾股定理(1)【教学目标】1.经历勾股定理的探索过程,掌握勾股定理的简单应用;2.经历观察、猜想、归纳和验证的数学发现过程,体会形数结合、化归的思想.【教学重点】探索和证明勾股定理,勾股定理的简单应用.【教学难点】勾股定理的探索和证明.【教学过程】一.课前导学:学生自学课本22-24页内容,并完成下列问题:1.【探究一】:观察图1,(1)你能找出图中正方形A、B、C面积之间的关系吗?(2)图中正方形A、B、C所围成的等腰直角三角形三边之间有什么特殊关系?2.【探究二】:如图2,每个小方格的边长均为1,(1)计算图中正方形A、B、C面积.【讨论】如何求正方形C的面积?(2)图中正方形A、B、C面积之间有何关系?(3)图中正方形A、B、C所围成的直角三角形三边之间有什么特殊关系?【猜想】:如果直角三角形的两条直角边长分别为a、b,斜边长为c,那么.二、合作、交流、展示:1.【探究三】:如图3,如何证明上述猜想?【温馨提示】:用两种方法表示出大正方形的面积.4.【探究四】:如图4,如何证明上述猜想?5.勾股定理:如果直角三角形的两条直角边长分别为a、b,斜边长为c,那么.文字叙述:.1图1图3图4图26.【探究五】:已知在Rt△ABC中,∠C=,(1)若;(2)若2;(3)若.(4)若3,.【勾股定理结论变形】:.7.【探究六】:若一个直角三角形的三边长为8,15,4,则=.三、巩固与应用1.如图5,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了步路(假设2步为1m),却踩伤了花草.2.如图6,分别以Rt△ABC的三边向外作正方形,其面积分别为5图5图6图7、、,且6,,则=.3.根据图7及提示证明勾股定理.:【提示】:三个三角形的面积和=一个梯形的面积.7四、小结:(1)勾股定理及其简单应用;(2)面积法证题与数形结合思想.五、作业:必做:P28习题T1、2、317.1勾股定理(2)【教学目标】能熟练运用勾股定理计算,会用勾股定理解决简单的实际问题.【教学重点】运用勾股定理计算与推理.【教学难点】将实际问题转化为数学问题解决.【教学过程】一.课前导学:学生自学课本25页内容,并完成下列问题:1.勾股定理:如果直角三角形的两条直角边长分别为a、b,斜边长为c,那么:8(或)变形:(或9)(或)2.填空题:在Rt△ABC,∠C=90°,⑴如果a=7,c=25,则b=;⑵如果∠A=30°,a=4,则b=;⑶如果∠A=45°,a=3,则c=;(4)如果b=8,a:c=3:5,则c=.3.【探究一】:一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?思考:①薄木板怎样好通过?;②在长方形ABCD中,是斜着能通过的最大长度;③薄模板能否通过,关键是比较10与的大小.解:在Rt△ABC中,根据勾股定理AC2=()2+()2=2+2=.[来源:学科网]因此AC=≈.因为AC(填“>”、“<”、或“=”)木板的宽2.2m,所以木板从门框内通过.(填:“能:或“不能:)4.【探究二】:如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?点拨:①梯子底端B随着梯子顶端A沿墙下滑而外移到D,那么的长度就是梯子外移的距离.②BD=-,求BD,关键是要求出和的长.③梯子在下滑的过程中,梯子的长度变了吗?④在Rt△AOB中,已知和,如何求OB?在Rt△COD中,已知和,如何求OD?你能将解答过程板书出来吗?二、合作、交流、展示:1.运用勾股定理解决实际问题的思路:实际问题数学问题2.如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行多少米?113.小东拿着一根长竹竿进一个宽3米的城门,他先横着拿进不去,又竖起来拿,结果竿比城门高1米,当他把竿斜着时,两端正好顶着城门的对角,问竿长几米?三、巩固与应用1.若直角三角形的两边长分别为3cm、4cm,则第三边长为.2.已知:如图,等边△ABC的边长是6cm.⑴求等边△ABC的高.⑵求S△ABC..3.如图,分别以Rt△ABC的三边为直径作半圆,其面积分别为、12DCBA、,且13,,则14=.4.如图,直线同侧有三个正方形、15、,若16、的面...