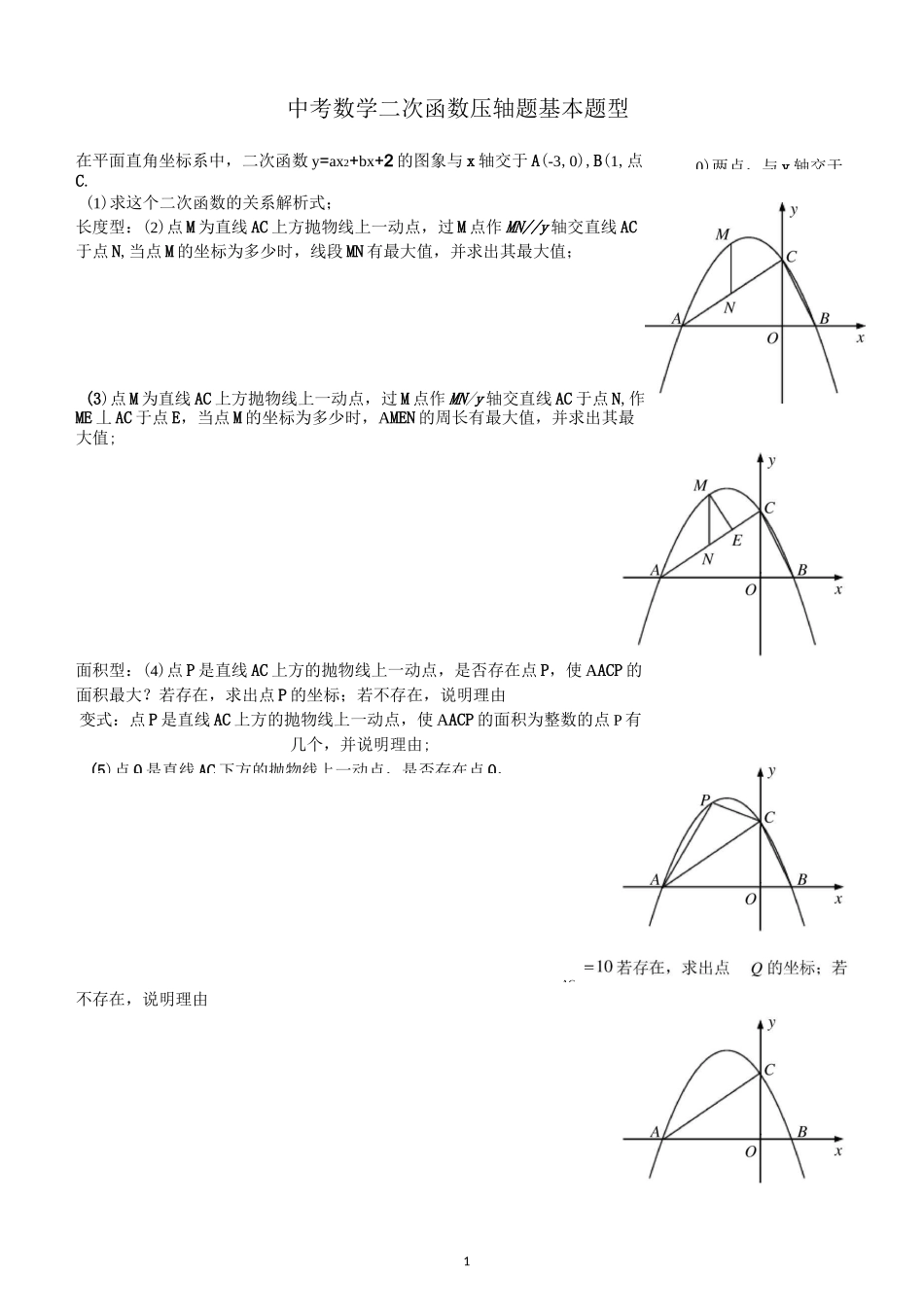
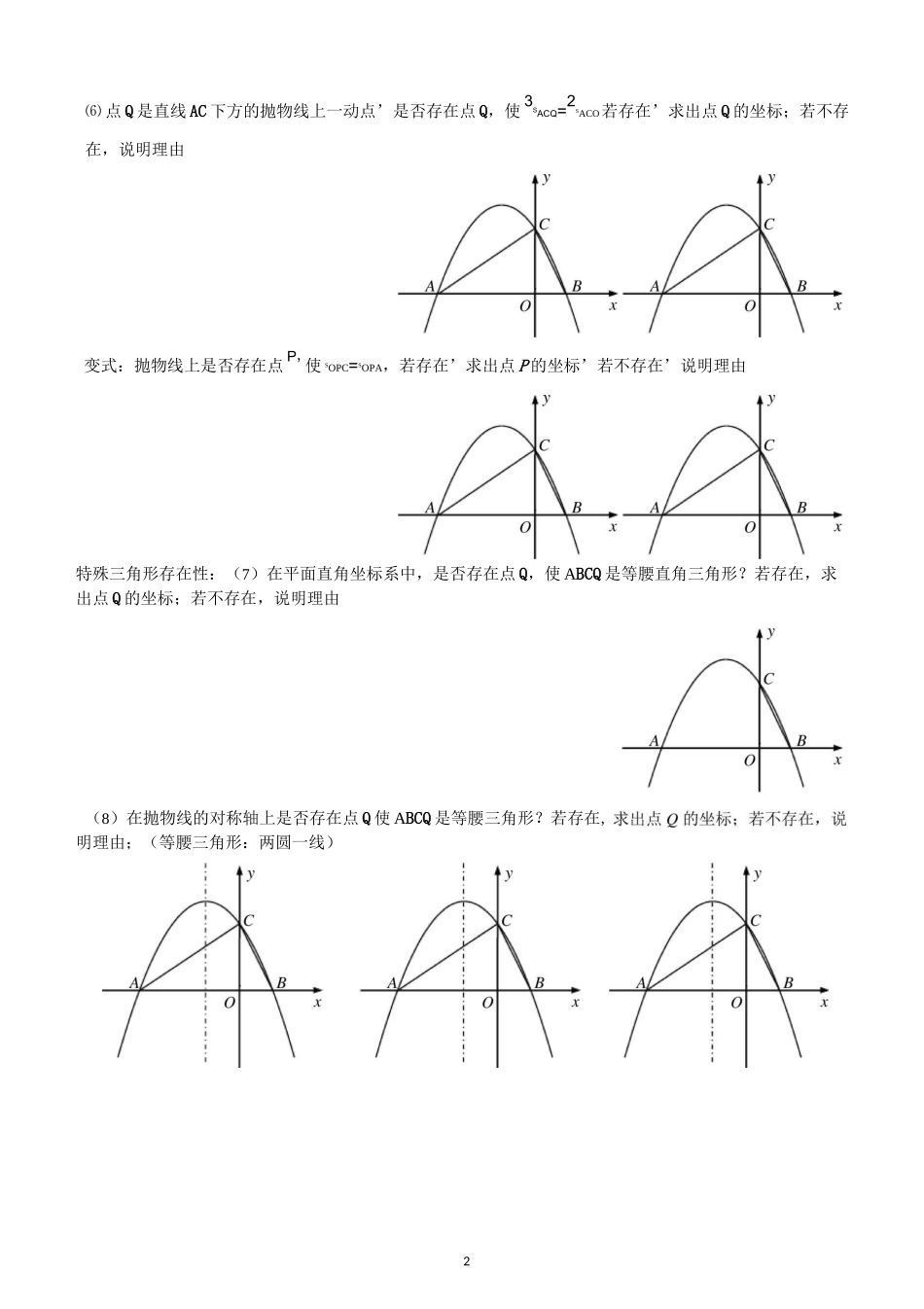
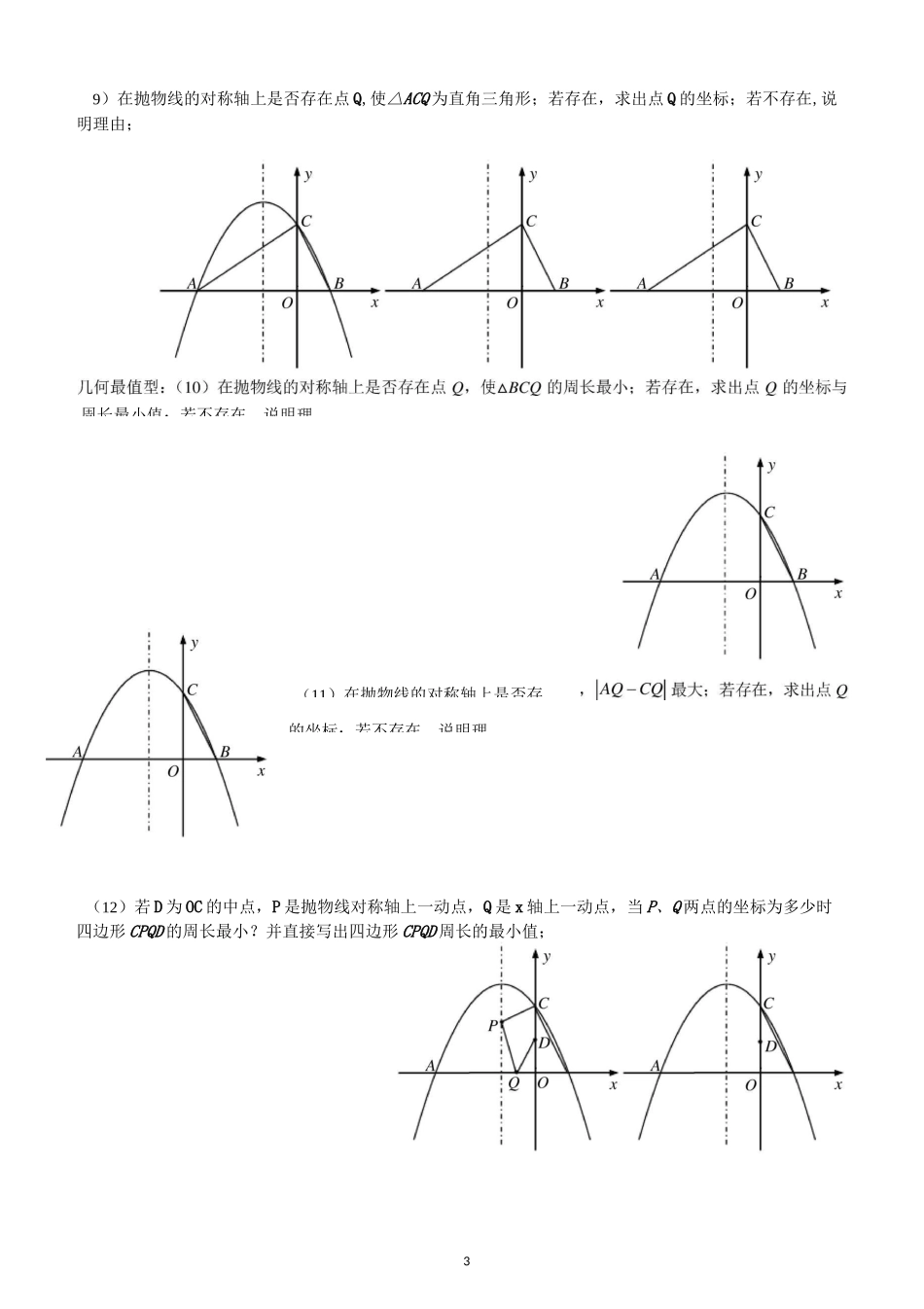
10)两点,与y轴交于(5)点Q是直线AC下方的抛物线上一动点,是否存在点Q,AC中考数学二次函数压轴题基本题型在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(-3,0),B(1,点C.(1)求这个二次函数的关系解析式;长度型:(2)点M为直线AC上方抛物线上一动点,过M点作MN//y轴交直线AC于点N,当点M的坐标为多少时,线段MN有最大值,并求出其最大值;(3)点M为直线AC上方抛物线上一动点,过M点作MN/y轴交直线AC于点N,作ME丄AC于点E,当点M的坐标为多少时,AMEN的周长有最大值,并求出其最大值;面积型:(4)点P是直线AC上方的抛物线上一动点,是否存在点P,使AACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由变式:点P是直线AC上方的抛物线上一动点,使AACP的面积为整数的点P有几个,并说明理由;不存在,说明理由2⑹点Q是直线AC下方的抛物线上一动点’是否存在点Q,使3SACQ=2SACO若存在’求出点Q的坐标;若不存在,说明理由变式:抛物线上是否存在点P'使SOPC=SOPA,若存在’求出点P的坐标’若不存在’说明理由特殊三角形存在性:(7)在平面直角坐标系中,是否存在点Q,使ABCQ是等腰直角三角形?若存在,求出点Q的坐标;若不存在,说明理由(8)在抛物线的对称轴上是否存在点Q使ABCQ是等腰三角形?若存在,明理由;(等腰三角形:两圆一线)(11)在抛物线的对称轴上是否存39)在抛物线的对称轴上是否存在点Q,使△ACQ为直角三角形;若存在,求出点Q的坐标;若不存在,说明理由;(12)若D为OC的中点,P是抛物线对称轴上一动点,Q是x轴上一动点,当P、Q两点的坐标为多少时四边形CPQD的周长最小?并直接写出四边形CPQD周长的最小值;周长最小值;若不存在,说明理的坐标;若不存在,说明理4相似存在性:(13)点Q是坐标轴上一动点,是否存在点Q,使以点B、O、Q为顶点的三角形与△AOC相似?若存在,求出点Q的坐标;若不存在,说明理由;14)点Q是抛物线上一动点,过点Q作QE垂直于x轴,垂足为E.是否存在点Q,使以点B、顶点的三角形与△AOC相似?若存在,角度问题:(15)抛物线上是否存在的点Q,使ZQCA=45°,若存在,求出Q点的坐标;若不存在,说明理由;EQ(17)在抛物线的对称轴上是否存在点Q到直线BC的距离与到x轴的距离相等?若存在求出点Q,若不存在请说明理由;(在抛物线的对称轴上是否存在点Q,使0Q与x轴和直线BC都相切?)5*变式:抛物线上是否存在的点Q,使ZQCA+ZOCB=45。,若存在,求出Q点的坐标;若不存在,说明理由;(19)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,特殊四边形存在性问题:(18)点M为抛物线上一动点,过M点作MN〃y轴交直线AC于点N,当以O、C、6(20)点Q是抛物线上一动点,点M为抛物线对称轴上一动点,当以A、C、M、Q为顶点的四边形是平行(21)Q为抛物线的对称轴上一动点,点P在坐标平面内,若以A、C、P、Q为顶点的四边形为矩形,求Q点的坐标;以A、C、P、Q为顶点的四边形能为正方形吗?若能,请直接写出此时Q点的坐标;(矩形存在点的坐标;(菱形存在性问题转化成等腰三角形存在性问题)