锐角三角函数2VIP免费

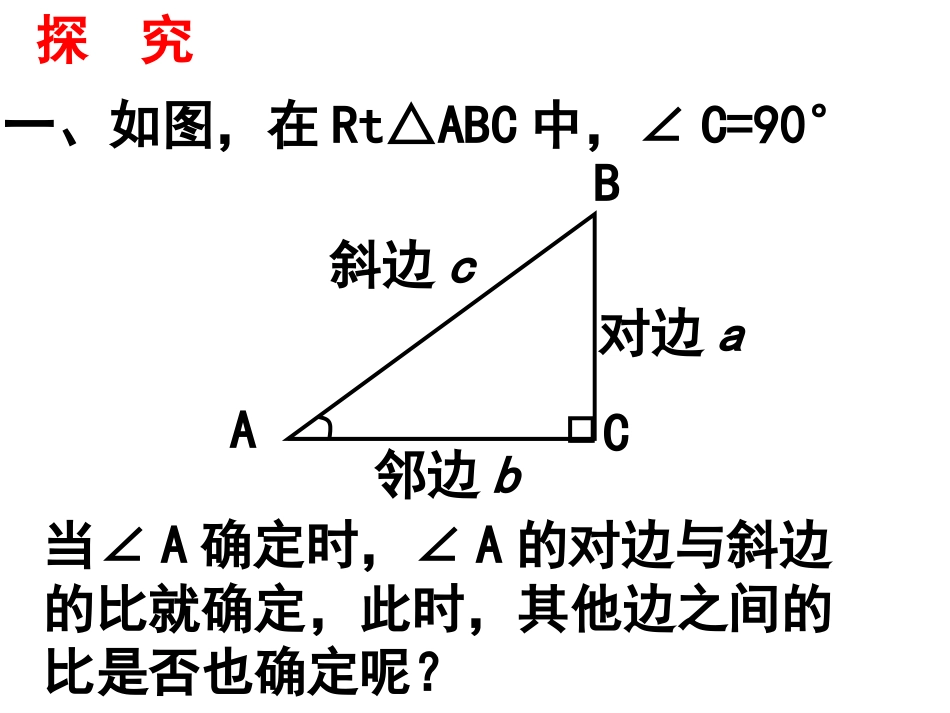
锐角三角函数(2)锐角三角函数(2)复习正弦的定义：在Rt△ABC中，∠C=90°，我们把锐角A的对边与斜边的比叫做∠A的正弦。记作sinA，即斜边的对边AAsinca探究一、如图，在Rt△ABC中，∠C=90°ACB对边a邻边b斜边c当∠A确定时，∠A的对边与斜边的比就确定，此时，其他边之间的比是否也确定呢？探究二、如图，Rt△ABC和Rt△A’B’C’中，∠C=∠C’=90°，∠A=∠A’=α，那么ACBA′C′B′与有什么关系？ABACBACAα探究三、如图，Rt△ABC和Rt△A’B’C’中，∠C=∠C’=90°，∠A=∠A’=α，那么ACBACB与有什么关系？αBCAC,,,,BCAC新授余弦的定义：在Rt△ABC中，∠C=90°，我们把锐角A的邻边与斜边的比叫做∠A的余弦。记作cosA，即斜边的邻边AAcoscb新授正切的定义：在Rt△ABC中，∠C=90°，我们把锐角A的对边与邻边的比叫做∠A的正切。记作tanA，即的邻边的对边AAAtanba巩固1、如图，分别求出下列两个直角三角形两个锐角的余弦值和正切值。ACB1312（1）23ACB（2）513巩固2、如图，在Rt△ABC中，如果各边长都扩大2倍，那么锐角A的余弦值和正切值有什么变化？为什么？ACBA’C’B’例1如图，在Rt△ABC中，∠C=90°，ACB653BC=6，sinA=，求cosA、tanA的值。练习1、如图，在RtABC△中，∠C=90°，43AB=10，tanA=，求sinA、cosA的值。ACB2、如图，在Rt△ABC中，∠C＝90°，cosA＝，求sinA、tanA的值．1517∵15cos17ACAAB88sin,1717BCkAABk88tan1515BCkAACkABC设AC=15k，则AB=17k所以2222(17)(15)8BCABACkkk解：如图在Rt△ABC中，例2.已知锐角α的始边在x轴的正半轴上(顶点在原点)，终边上一点的坐标为(1，2)，求角α的三个三角函数值。xoyP(1,2)αA225sin55a==15cos55a==tan2a=新授三角函数的定义：锐角A的正弦、余弦、正切统称为锐角三角函数。对于锐角A的每一个确定的值，sinA有唯一的值与它对应，所以sinA是A的函数。同样地，cosA、tanA也是A的函数。=ac斜边的对边AsinA=知识提升在Rt△ABC中=bc斜边的邻边AcosA==ab的邻边的对边AAtanA=所以，对于任何一个锐角α，有0＜sinα＜1，0＜cosα＜1，tanα＞0，bABCa┌csinaAccosbAc公式一∠A+B=90∠°时，sinA=cosBcosA=sinB公式二公式三22sinAcosA1sinAtanAcosAtanAtanB=1·tanaAb=sinbBccosaBctanbBa=巩固4、直角三角形的斜边和一条直角边的比为25∶24，则其中最小的角的正切值为。3、如果α是锐角，且cosα=，那么sin(90°-α)的值等于()53A.B.C.D.25954532516724C巩固5、如图，在四边形ABCD中，∠BAD=BDC=90°∠，且AD=3，sinABD∠53=，sinDBC=∠，求AB、BC、1312CD的长。ACBD巩固6、如图，为测河两岸相对两电线杆A、B的距离，在距A点17米的C处(AC⊥AB)测得∠ACB=50°，则A、B间的距离为()A.17sin50°米B.17cos50°米C.17tan50°米D.34sin50°米ACBc小结1.余弦的定义：斜边的邻边AAcoscb2.正切的定义：的邻边的对边AAAtanab3.三角函数的定义作业:1、完成自能P61-631~11题2、选做12题的值求若sincos3sin2cos5,2tan1、扩展：02020015cos15sin263tan27tan2、