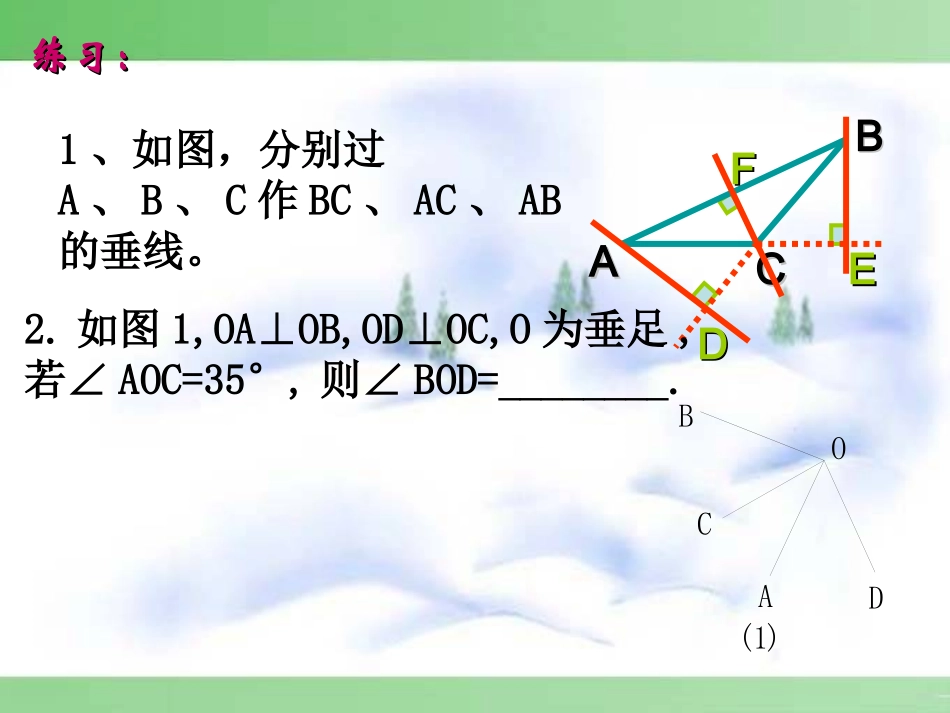
5.1.2垂线(2)1、垂直的定义4、垂线的画法5、垂线的性质(1)在同一平面内过一点有且只有一条直线与已知直线垂直一、放;二、靠;三、移;四、画复习当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。22..垂直的表示垂直的表示3,垂直的书写“垂直”90°想ab⊥ab⊥或或bb⊥⊥a,a,66注意注意::((11))过一点画已知线段过一点画已知线段((或射线或射线))的垂线的垂线,,就就是画这条线段是画这条线段((或射线或射线))所在直线的垂线所在直线的垂线..((22))过一点向已知线段作垂线,则垂足一定在已知线段上或在线段的延长线上(3)垂线是直线不是线段和射线练习:练习:1、如图,分别过A、B、C作BC、AC、AB的垂线。AABBCCDDEEFF2.如图1,OA⊥OB,OD⊥OC,O为垂足,若∠AOC=35°,则∠BOD=________.(1)ODCBA问题:在灌溉时,要把河中的水引到农田P处,如何挖掘能使渠道最短?思考:(1)你能将这个实际问题转化成数学问题吗?(2)在直线上有无数个点,试着取几个点与点P相连,比较一下它们的大小关系.你有什么发现?(3)你能猜想一下最短的位置会在哪儿?它唯一吗?为什么?(4)你能用一句话总结出观察得出的结论吗?此问题就是此问题就是“直线外“直线外一点与已知直线上一点与已知直线上各点所连的线段中各点所连的线段中,,有没有最短的线有没有最短的线段段?”?”PlABCDE∟结论结论::垂线性质(垂线性质(22))连接直线外一点与直线连接直线外一点与直线上各点的所有线段中,上各点的所有线段中,垂线垂线段最短段最短..简单说成简单说成::垂线段最短垂线段最短..1、垂线段的概念:由直线外一点向直线引由直线外一点向直线引垂线,这点与垂足间的垂线,这点与垂足间的线段线段叫做叫做垂线段垂线段。。PPllAA22、点到直线的距离:、点到直线的距离:直线外一点到这条直线的垂线段的直线外一点到这条直线的垂线段的长度长度,叫做,叫做点到直线的距离。点到直线的距离。PPllAA思考:如图是一个同学跳远的位置思考:如图是一个同学跳远的位置,,跳远成绩怎么量跳远成绩怎么量??lPA解解::过过PP点作点作PA⊥PA⊥ll于点于点AA,,垂线垂线段段PAPA的的长度长度就是该同就是该同学的跳远成绩学的跳远成绩..思考:(5)现在,你知道水渠怎么挖了吗?如果图中的比例尺为1:100000,水渠大概要挖多长?(6)你能列举生活中类似的实例吗?例1、如图,点M、N分别在直线AB、CD上,用三角板画图,1)过M点画CD的垂线交CD于F点,2)M点和N点的距离是线段____的长,3)M点到CD的距离是线段____的长。MNMFABCDMNF练习:已知直线a、b,过a上一点M作MNa,⊥交b于点N,过N作NQb⊥交a上于点Q.请说出哪一条线段的长是哪一点到哪一条直线的距离?并且用刻度尺测量这个距离.baMNQ例2、如图,ABC=90∠°,1=60∠°,过B作AC的垂线BO,垂足是O,过O作BC的垂线,垂足是D,若∠1=2,∠求∠ABO,BOD∠的度数.12ABCDO BOBO⊥AC⊥AC于于OO点点))(已知)(已知) ∠ ∠ABC=90ABC=90°()°()∠∠1=60°1=60°()()已知已知∴∠∴∠ABO=30°ABO=30°解:解:(已知)(已知)∴∠∴∠BOC=90°BOC=90°∴∠∴∠BOD=30°BOD=30°(余角定义)(余角定义)(余角定义)(余角定义)已知已知(垂直定义)(垂直定义)又 又 ∠∠2=∠1=60°2=∠1=60°ABCD1、下列说法正确的是()(A)线段AB叫做点B到直线AC的距离。(B)线段AB的长度叫做点A到直线AC的距离(C)线段BD的长度叫做点D到直线BC的距离(D)线段BD的长度叫做点B到直线AC的距离D练习2.如图,AC⊥BC,C为垂足,CD⊥AB,D为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC=6,那么点C到AB的距离是_______,点A到BC的距离是________,点B到CD的距离是_____,A、B两点的距离是_________.DCBA想一想:如图,在线段AB、AC、AD、AE、AF中AD最短.小明说垂线段最短,因此线段AD的长是点A到BF的距离,对小明的说法,你认为_________________.FEDCBA小明的说法不对,只有ADBF⊥,才可以说线段AD的长是点A到BF的距离。3、已知点A,与点A的距离是5cm的直线可画()A.1条B.2条C.3条D.无数条D4如图:AC⊥BC于C,CD⊥AB于D,DE⊥BC...