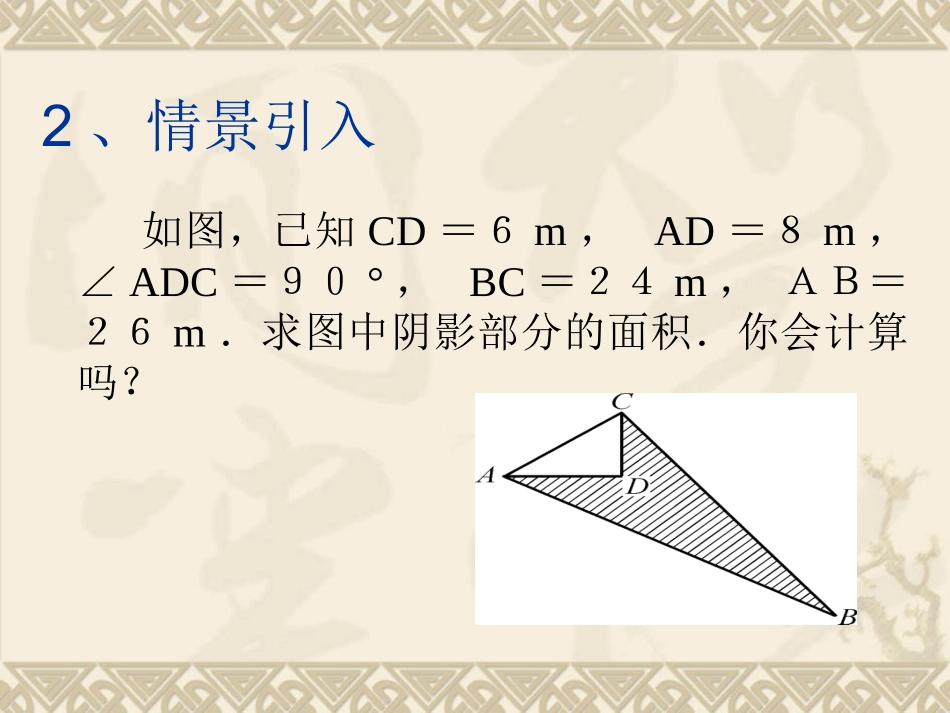
14.2勾股定理的应用(二)1、勾股定理及其逆定理的内容是什么?勾股定理:直角三角形两直角边的平方和等于斜边的平方。勾股定理的逆定理:如果三角形的三边长有关系a2+b2=c2,那么这个三角形是直角三角形,且边c所对的角为直角.一、复习2、情景引入如图,已知CD=6m,AD=8m,∠ADC=90°,BC=24m,AB=26m.求图中阴影部分的面积.你会计算吗?二、自探一如图14.2.5,在3×3的正方形网格中,每个小正方形的边长都为1,请在给定网格中按下列要求画出图形:(1)画出所有从点A出发,另一个端点在格点(即小正方形的顶点)上,切长度为的线段;(2)画出所有的以题(1)中所画线段的等腰三角形。图14.2.5图14.2.5图14.2.6图14.2.6DDBBCCEE合探一1、解:(1)图14.2.6中,AB、AC、AE、AD的长度均为.(2)图14.2.6中,△ABC、△ABE、△ABD、△ACE、△ACD、△AED就是所要画的等腰三角形.自探二如图14.2.7,已知CD=6m,AD=8m,∠ADC=90°,BC=24m,AB=26m.求图中阴影部分的面积.图14.2.7合探二解:在RtADC△中,∵AC=AD+CD=6+8=100(勾股定理),∴AC=10m.∵AC+BC=10+24=676=26=AB∴△ACB为直角三角形(勾股定理的逆定理)∴S阴影部分=S△ACB-S△ACD=1/2×10×24-1/2×6×8=96(m)质疑再探对于本节课的学习,你还有哪些疑问?请大胆提出来,让我们一起来探讨。运用拓展1、请同学们仿照例题,自编一道运用勾股定理及其逆定理的内容来解决的问题,让你的同桌来解答。看谁编写的题最好。2、教师预设习题(1)在RtABC△中,∠B=90°,BC=15,AC=17,以AB为直径作半圆,则此半圆的面积为_________(2)直角三角形三边的长分别为3、4、x,则x可能取的值有().A.1个B.2个C.3个D.无数多个(1)如图1,一个梯子AB长2.5m,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5m,梯子滑动后停在DE的位置上,如图2,测得BD长为0.5m,求梯子顶端A下落了多少米.图1图2解法指导:直角三角形中,已知一直角边和斜边是勾股定理的重要应用之一.勾股定理:a2+b2=c2的各种变式:a2=c2-b2,b2=c2-a2.应牢固掌握,灵活应用.分析:先利用勾股定理求出AC与CE的长,则梯子顶端A下落的距离为AE=AC-CF.解:在RtABC△中,AB2=AC2+BC2∴2.52=AC2+1.52,∴AC=2(m).在RtEDC△中,DE2=CE2+CD2,∴2.52=CE2+22∴CE2=2.25,∴CE=1.5(m),∴AE=AC-CE=2-1.5=0.5(m)答:梯子顶端A下落了0.5m.小结本节课是是运用勾股定理和判定直角三角形的勾股逆定理来解决实际问题,解决这类问题的关键是画出正确的图形,通过数形结合,构造直角三角形,碰到空间曲面上两点间的最短距离间题,一般是化空间问题为平面问题来解决.即将空间曲面展开成平面,然后利用勾股定理及相关知识进行求解,遇到求不规则面积问题,通常应用化归思想,将不规则问题转换成规则何题来解决.解题中,注意辅助线的使用.特别是“经验辅助线”的使用.