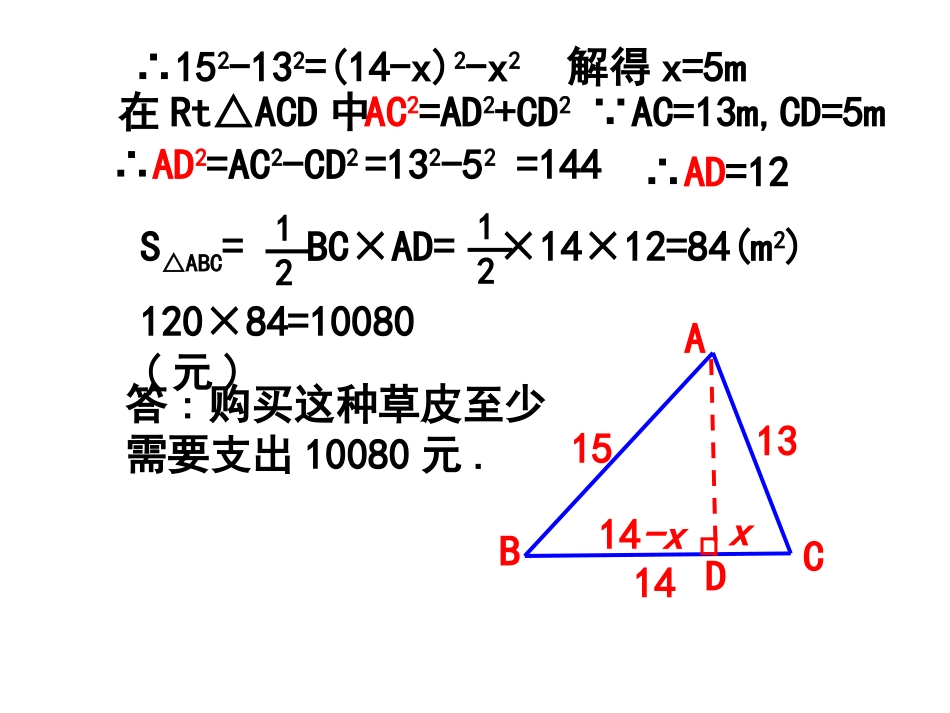
17.3勾股定理的应用校园里有一块三角形空地校园里有一块三角形空地,,现准备在这块现准备在这块空地上种植草皮以美化环境空地上种植草皮以美化环境,,已经测量出已经测量出它的三边长分别是它的三边长分别是13,14,1513,14,15米米,,若这种草若这种草皮每平方米售价皮每平方米售价120120元元,,则购买这种草皮则购买这种草皮至少需要支出多少元至少需要支出多少元??151314ABCDx14-x解:过点A作AD⊥BC于D,设CD=xm,则BD=(14-x)m在Rt△ABD中∴AD2=AB2-BD2()在Rt△ACD中∴AD2=AC2-CD2()∴AB2-BD2=AC2-CD2∴152-(14-x)2=132-x2151314ABCDx14-x∴152-132=(14-x)2-x2解得x=5m在Rt△ACD中AC2=AD2+CD2∵AC=13m,CD=5m∴AD2=AC2-CD2=132-52=144∴AD=12120×84=10080(元)S△ABC=BC×AD=×14×12=84(m2)1212答:购买这种草皮至少需要支出10080元.如图,是一块四边形绿地示意图,其中AB长24米,BC长20米,CD长15米,DA长7米,∠C=90°求绿地ABCD的面积.CBAD242015725ABCDEF如图,在长方形ABCD中,若已知AB=8cm,BC=10cm,将AD沿直线AF折叠,使点D落在BC上的点E处(1)求CE的长.(2)求CF的长.解:(1)∵长方形ABCD,AB=8cm,BC=10cm∴CD=AB=8cm,AD=BC=10cm∵AD沿直线AF折叠,点D落在BC上的点E处∴EF=DF,AE=AD=10cm在Rt△ABE中∵∠B=90°∴AB2+BE2=AE2()∵AB=8cm,AE=10cm∴BE2=AE2-AB2=102-82=36∵AC>0∴AC=8∴BE=6ABCDEF∵AC>0∴AC=8CE=BC-BE=10-6=4cm(2)设EF=DF=xcm,则CF=(8-x)cm在Rt△ECF中∵∠C=90°∴CE2+CF2=EF2()∴42+(8-x)2=x2,解得x=5cmCF=CD-DF=8-5=3cmxx8-x(勾股定理是列方程的依据)如图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段,现在老师想知道旗杆的高度,你能帮老师想个办法吗?请你与同伴交流设计方案?CABDE如图,小颖同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,求出CE的长.解:连结BE设CE=xcm,则BE=AE=(10-x)cm由已知可知:DE是AB的中垂线∴AE=BE在Rt△ABC中,∵∠C=90°x10-x10-x∴BE2=BC2+CE2(10-x)2=62+x2解得x=3.2即CE=3.2cm下面以a,b,c为边长的△ABC是不是直角三角形?如果是,那么哪一个角是直角?(1)a=25b=20c=15;(2)a=13b=14c=15;(3)a:b:c=3:4:5请你说出几组勾股数常见的勾股数组(笔记)勾股弦34551213724258151794041116061勾股弦345681091215121620152025182430常见的勾股数组如图,为了测得湖两岸点A和点C间的距离,一个观测者在点B设立了一根标杆,使∠ACB=90°.测得AB=200m,CB=160m.根据测量结果,求A、C两点间的距离.ACB工人在制作铝合金窗框时,为保证窗框的四个角都是直角,有时采用如下的方法:如图,先量出框AB、BC的长,再量出两点A、C的距离,由此推断∠B是否为直角.1.推断∠B是否为直角的依据是什么?2.如果AB=1.2m,BC=0.9m,那么只有当AC多长时,∠B为直角呢?BCA判断题.1.ABC的两边AB=5,AC=12,则BC=13()2.ABC中a=6,b=8,则c=10()2.等腰三角形的周长是20cm,底边上的高是6cm,则底边的长为_____cm.1.在ABC中,∠C=90°,若AC=6,CB=8,则ABC面积为_____,斜边为上的高为_____.有一个圆柱体,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A点相对的B处的食物,需要爬行的最短路程是多少?ABABC