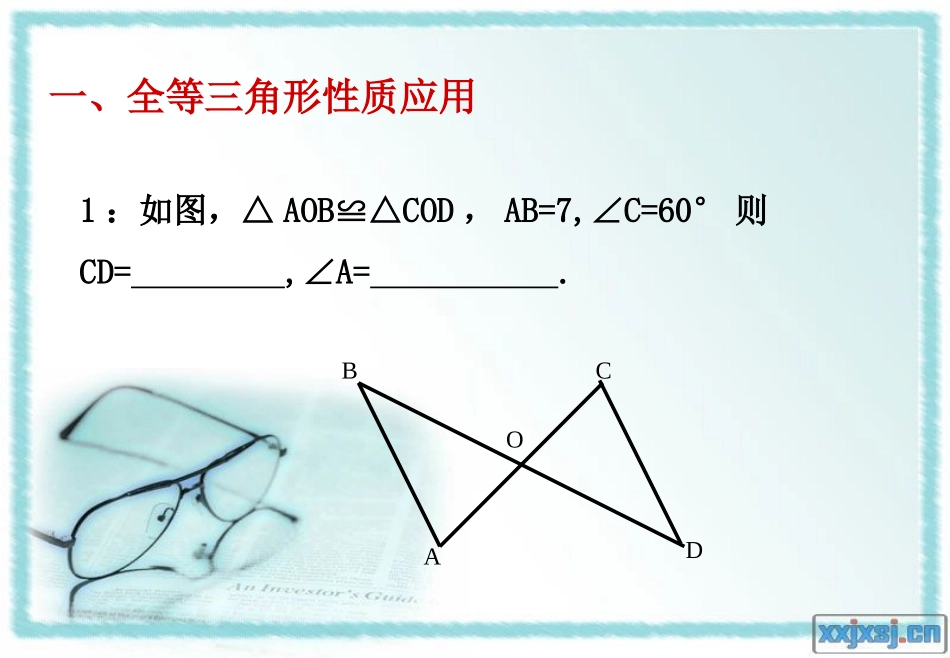
《数学》(北师大.七年级下册)议论堡中学张云仿一、全等三角形概念:能够的三角形是全等三角形.二、全等三角形性质:全等三角形对应边.全等三角形对应角.3、全等三角形的识别:(1)一般三角形全等的识别:SSS,SAS,ASA,AAS(2)直角三角形全等的识别:除以上方法外,还有HL注意:1、“分别对应相等”是关键2、两边及其中一边的对角分别对应相等的两个三角形不一定全等一、全等三角形性质应用1:如图,△AOB≌△COD,AB=7,∠C=60°则CD=,∠A=.ABCDO一、全等三角形性质应用2:已知△ABC≌△DEF,∠A=60°,∠C=50°则∠E=.CBAFED一、全等三角形性质应用3:如图,△ABCDEF≌△,DE=4,AE=1,则BE的长是()A.5B.4C.3D.2FEDCBA1、如图所示,:已知AC=AD,请你添加一个条件————,使得△ABC≌△ABDBACD思路思路已知两边找另一边(SSS)找夹角(SAS)隐含条件AB=AB二、全等三角形判定变式1:如图,已知∠C=D∠,请你添加一个条件————,使得△ABC≌△ABDBACD思路思路已知一边一角这边为角的对边找任一角(AAS)隐含条件AB=AB变式2:如图,已知∠CAB=DAB∠,请你添加一个条件————,使得△ABC≌△ABDBACD思路思路已知一边一角这边为角的邻边夹角的另一边(SAS)夹边的另一角(ASA)找边的另一角(AAS)隐含条件AB=AB如图,已知∠B=E∠,要识别△ABCAED≌△,需要添加的一个条件是--------------思路已知两角:找夹边找一角的对边ABCDEAB=AEAC=AD或DE=BC(ASA)(AAS)课堂练习课堂练习::已知已知::如图如图∠∠B=DEF,BC=EF∠B=DEF,BC=EF∠,,补充条件补充条件求证求证::ΔABCΔABC≌≌ΔDEFΔDEF∠∠ACB=DEF∠ACB=DEF∠AB=DEAB=DEAB=DEAB=DE、、AC=DFAC=DFAABBCCDDEEFF====DDEEFFAABBCC∠∠A=D∠A=D∠(1)(1)若要以“若要以“SAS”SAS”为依据,还缺条件_____为依据,还缺条件_____;;(2)(2)若要以“若要以“ASA”ASA”为依据,还缺条件____;为依据,还缺条件____;(4)(4)若要以“若要以“SSS”SSS”为依据,还缺条件_____;为依据,还缺条件_____;(3)(3)若要以“若要以“AAS”AAS”为依据,还缺条件_____为依据,还缺条件_____;;(5)(5)若若∠∠B=DEF=90°∠B=DEF=90°∠要以“要以“HLHL””为依据,为依据,还缺条件_____还缺条件_____AC=DF二小试牛刀1.如图,在△ABC和△BAD中,BC=AD,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是.DABC二、小试牛刀ABCEF2.已知:如图,△AEF与△ABC中,∠E=B,∠EF=BC.请你添加一个条件,使△AEFABC.≌△小试牛刀例2、如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是拿()去配.三、利用全等三角形证明线段(角)相等例1.如图,已知AB=AD,AC=AE,∠1=∠2,求证:BC=DEABCDE12请同学们注意书写格式哦!三、利用全等三角形证明线段(角)相等2.如图,点B、E、C、F在一条直线上,AB=DE,ABDE∥,∠A=∠D.求证:BE=CF.FEDCBA证明两条线段相等的方法有哪些?DCBA3.已知:如图,△ABC和△CDB中,AB=DC,AC=DB求证:∠ABD=DCA∠三、利用全等三角形证明线段(角)相等O证明两个角相等的方法有哪些?1.如图,在△AFD和△BEC中,点A、E、F、C在同一直线上,有下列四个论断:①AD=CB,②AE=CF,③∠B=∠D,④∠A=∠C.请用其中三个作为条件,余下一个作为结论,编一道数学问题,并写出解答过程。ABCDEF四、综合应用在△ABC中,ACB=90°,AC=BC,∠直线MN经过点C,ADMN⊥于点D,BEMN⊥于点E,(1)当直线MN旋转到图(1)的位置时,猜想线段AD,BE,DE的数量关系,并证明你的猜想NMEDCBA图(1)在△ABC中,ACB=90°,AC=BC,∠直线MN经过点C,ADMN⊥于点D,BEMN⊥于点E,(2)当直线MN旋转到图(2)的位置时,猜想线段AD,BE,DE的数量关系,并证明你的猜想NMEDCBA图(2)感悟与反思:1、平行——角相等;2、对顶角——角相等;3、公共角——角相等;4、角平分线——角相等;5、垂直——角相等;6、中点——边相等;7、公共边——边相等;8、旋转——角相等,边相等。1、要说明两个三角形全等,要结合题目的条件和结论,选择恰当的判定方法2、全等三角形,是说...